Question

\[\frac{dy}{dx}\] + y cos x = sin x cos x

Answer 1

We have, 
\[\frac{dy}{dx} + y \cos x = \sin x \cos x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
where
\[P = \cos x\]
\[Q = \sin x \cos x\]
\[ \therefore I.F. = e^{\int P\ dx} \]
\[ = e^{\int\cos x\ dx} \]
\[ = e^{\sin x} \]
\[\text{Multiplying both sides of }\left( 1 \right)\text{ by }e^{\sin x} ,\text{ we get }\]
\[ e^{\sin x} \left( \frac{dy}{dx} + y \cos x \right) = e^{\sin x} \sin x \cos x\]
\[ \Rightarrow e^{\sin x} \frac{dy}{dx} + e^{\sin x} y \cos x = e^{\sin x} \sin x\cos x \]
Integrating both sides with respect to x, we get
\[y\ e^{\sin x} = \int e^{\sin x} \sin x\cos \text{ x } dx + C\]
\[ \Rightarrow y e^{\sin x} = I + C . . . . . \left( 2 \right)\]
where
\[I = \int e^{\sin x} \sin x \cos \text{ x } dx\]
\[\text{Putting }t = \sin x,\text{ we get }\]
\[dt = \cos \text{ x }dx\]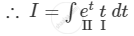

\[ = t\int e^t dt - \int\left[ \frac{d}{dt}\left( t \right)\int e^t dt \right]dt\]
\[ = t e^t - e^t \]
\[ = e^t \left( t - 1 \right)\]
\[ = e^{\sin x} \left( \sin x - 1 \right)\]
\[\text{Putting the value of I in }\left( 2 \right), \text{we get }\]
\[\text{ y } e^{\sin x} = e^{\sin x} \left( \sin x - 1 \right) + C\]
\[ \Rightarrow y = \sin x - 1 + C e^{- \sin x} \]
\[\text{Hence, }y = \sin x - 1 + C e^{- \sin x}\text{ is the required solution.}\]