Advertisements
Advertisements
प्रश्न
Discuss the continuity of the following function at the point(s) or on the interval indicated against them:
f(x) = [x + 1] for x ∈ [−2, 2)
Where [*] is greatest integer function.
उत्तर
f(x) = [x + 1] ; x ∈ [−2, 2)
∴ f(x) `{:(= -1 , ";" x ∈ [−2"," -1)),(= 0, ";" x ∈ [−1"," 0)),(= 1, ";" x ∈ [0"," 1)),(= 2, ";" x ∈ [1 "," 2)):}`
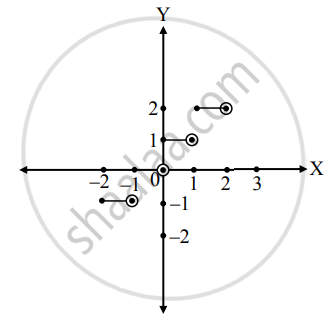
For continuity at x = – 1
`lim_(x -> -1^-) "f"(x) = lim_(x -> -1^-) [x + 1]`
`lim_(x -> -1^+) "f"(x) = lim_(x -> -1^+) [x + 1]`
∴ `lim_(x -> -1^-) "f"(x) = lim_(x -> -1^+) "f"(x)`
∴ f(x) is discontinuous at x = – 1
Similarly f(x) is discontinuous at
The points x = 0 and x = 1
APPEARS IN
संबंधित प्रश्न
Examine whether the function is continuous at the points indicated against them:
f(x) = x3 − 2x + 1, for x ≤ 2
= 3x − 2, for x > 2, at x = 2
Identify discontinuities for the following function as either a jump or a removable discontinuity :
f(x) `{:(= 4 + sin x",", "for" x < pi),(= 3 - cos x",", "for" x > pi):}`
Show that following function have continuous extension to the point where f(x) is not defined. Also find the extension :
f(x) = `(3sin^2 x + 2cos x(1 - cos 2x))/(2(1 - cos^2x)`, for x ≠ 0
Discuss the continuity of the following function at the point indicated against them :
f(x) `{:(=(4^x - 2^(x + 1) + 1)/(1 - cos 2x)",", "for" x ≠ 0),(= (log 2)^2/2",", "for" x = 0):}}` at x = 0.
If f(x) = `(cos^2 x - sin^2 x - 1)/(sqrt(3x^2 + 1) - 1)` for x ≠ 0, is continuous at x = 0 then find f(0)
If f(x) = `(4^(x - π) + 4^(π - x) - 2)/(x - π)^2` for x ≠ π, is continuous at x = π, then find f(π).
If f(x) `{:(= (24^x - 8^x - 3^x + 1)/(12^x - 4^x - 3^x + 1)",", "for" x ≠ 0), (= "k"",", "for" x = 0):}}` is continuous at x = 0, find k
If f(x) `{:(= (sin2x)/(5x) - "a"",", "for" x > 0),(= 4 ",", "for" x = 0),(= x^2 + "b" - 3",", "for" x < 0):}}` is continuous at x = 0, find a and b
For what values of a and b is the function
f(x) `{:(= (x^2 - 4)/(x - 2)",", "for" x < 2),(= "a"x^2 - "b"x + 3",", "for" 2 ≤ x < 3),(= 2x - "a" + "b"",", "for" x ≥ 3):}}` continuous for every x on R?
Determine the values of p and q such that the following function is continuous on the entire real number line.
f(x) `{:(= x + 1",", "for" 1 < x < 3),(= x^2 + "p"x + "q"",", "for" |x - 2| ≥ 1):}`
Show that there is a root for the equation 2x3 − x − 16 = 0 between 2 and 3.
Show that there is a root for the equation x3 − 3x = 0 between 1 and 2.
Select the correct answer from the given alternatives:
f(x) = `{:(= (2^(cotx) - 1)/(pi - 2x)",", "for" x ≠ pi/2),(= log sqrt(2)",", "for" x = pi/2):}`
Select the correct answer from the given alternatives:
If f(x) `{:(= "a"x^2 + "b"x + 1",", "for" |x −1| ≥ 3), (= 4x + 5",", "for" -2 < x < 4):}` is continuous everywhere then,
Discuss the continuity of the following function at the point(s) or on the interval indicated against them:
f(x) = `(cos4x - cos9x)/(1 - cosx)`, for x ≠ 0
f(0) = `68/15`, at x = 0 on `- pi/2 ≤ x ≤ pi/2`
Discuss the continuity of the following function at the point(s) or on the interval indicated against them:
f(x) `{:(= (|x + 1|)/(2x^2 + x - 1)",", "for" x ≠ -1),(= 0",", "for" x = -1):}}` at x = – 1
Identify discontinuity for the following function as either a jump or a removable discontinuity on their respective domain:
f(x) `{:(= x^2 + 5x + 1"," , "for" 0 ≤ x ≤ 3),(= x^3 + x + 5"," , "for" 3 < x ≤ 6):}`
Identify discontinuity for the following function as either a jump or a removable discontinuity on their respective domain:
f(x) `{:(= (x^2 + x + 1)/(x + 1)"," , "for" x ∈ [0, 3)),(=(3x +4)/(x^2 - 5)"," , "for" x ∈ [3, 6]):}`
Discuss the continuity of the following function at the point or on the interval indicated against them. If the function is discontinuous, identify the type of discontinuity and state whether the discontinuity is removable. If it has a removable discontinuity, redefine the function so that it becomes continuous:
f(x) = `((x + 3)(x^2 - 6x + 8))/(x^2 - x - 12)`
Find k if following function is continuous at the point indicated against them:
f(x) `{:(= ((5x - 8)/(8 - 3x))^(3/(2x - 4))",", "for" x ≠ 2),(= "k"",", "for" x = 2):}}` at x = 2
Find a and b if following function is continuous at the point or on the interval indicated against them:
f(x) `{:(= (4tanx + 5sinx)/("a"^x - 1)",", "for" x < 0),(= (9)/(log2)",", "for" x = 0),(= (11x + 7x*cosx)/("b"^x - 1)",", "for" x > 0):}`
Find f(a), if f is continuous at x = a where,
f(x) = `(1 - cos[7(x - pi)])/(5(x - pi)^2`, for x ≠ π at a = π
If f(x) = `{((x^4 - 1/81)/(x^3 - 1/27), x ≠ 1/3), (k, x = 1/3):}` is continuous at x = `1/3`, then the value of k is ______
If f(x) = `[tan (pi/4 + x)]^(1/x)`, x ≠ 0 at
= k, x = 0 is continuous x = 0. Then k = ______.
Let f : [-1, 2] → [0, ∞] be a continuous function such that f(x) = f(1 - x) ∀ x ∈ [-1, 2].
Let R1 = `int_-1^2 xf(x) dx` and R2 be the area of the region bounded by y = f(x), x = -1, x = 2 and the X-axis. Then, ______
If f(x) = `1/(1 - x)`, the number of points of discontinuity of f{f[f(x)]} is ______.
If the function f(x) = `[tan(π/4 + x)]^(1/x)` for x ≠ 0 is = K for x = 0 continuous at x = 0, then K = ?
If f(x) = `{{:(log(sec^2 x)^(cot^2x)",", "for" x ≠ 0),(K",", "for" x = 0):}`
is continuous at x = 0, then K is ______.
For what value of k, the function defined by
f(x) = `{{:((log(1 + 2x)sin^0)/x^2",", "for" x ≠ 0),(k",", "for" x = 0):}`
is continuous at x = 0 ?
Which of the following is not continuous for all x?
The function f(x) = x – |x – x2| is ______.
If f(x) = `{{:((x - 4)/(|x - 4|) + a",", "for" x < 4),(a + b",", "for" x = 4 "is continuous at" x = 4","),((x - 4)/(|x - 4|) + b",", "for" x > 4):}`
then ______.
For x > 0, `lim_(x rightarrow 0) ((sin x)^(1//x) + (1/x)^sinx)` is ______.
