Advertisements
Advertisements
प्रश्न
Find the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1.
उत्तर
Let A (2, 0), B (0, 3) be the given points.
Slope of AB = m1
= \[\frac{3 - 0}{0 - 2}\]
= \[\frac{- 3}{2}\]
Slope of the line x + y = 1 is -1
\[\therefore m_2 = - 1\]
Let \[\theta\] be the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1
\[\therefore \tan \theta = \left| \frac{m_1 - m_2}{1 + m_1 m_2} \right|\]
\[ = \left| \frac{- \frac{3}{2} + 1}{1 + \frac{3}{2}} \right|\]
\[ = \frac{1}{5}\]
\[ \Rightarrow \theta = \tan^{- 1} \left( \frac{1}{5} \right)\]
Hence, the acute angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1 is
\[\tan^{- 1} \left( \frac{1}{5} \right)\].
APPEARS IN
संबंधित प्रश्न
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
The slope of a line is double of the slope of another line. If tangent of the angle between them is `1/3`, find the slopes of the lines.
Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is
- Parallel to the x-axis,
- Parallel to the y-axis,
- Passing through the origin.
Find the slope of a line passing through the following point:
(3, −5), and (1, 2)
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (5, 6) and (2, 3); through (9, −2) and (6, −5)
What can be said regarding a line if its slope is negative?
Without using Pythagoras theorem, show that the points A (0, 4), B (1, 2) and C (3, 3) are the vertices of a right angled triangle.
If three points A (h, 0), P (a, b) and B (0, k) lie on a line, show that: \[\frac{a}{h} + \frac{b}{k} = 1\].
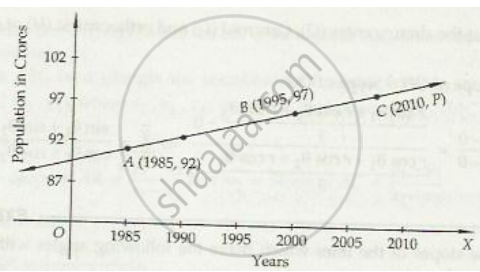
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
Find the angle between the X-axis and the line joining the points (3, −1) and (4, −2).
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear.
A quadrilateral has vertices (4, 1), (1, 7), (−6, 0) and (−1, −9). Show that the mid-points of the sides of this quadrilateral form a parallelogram.
Find the equation of a straight line with slope 2 and y-intercept 3 .
Find the equation of a straight line with slope − 1/3 and y-intercept − 4.
Find the equations of the bisectors of the angles between the coordinate axes.
Find the equation of the perpendicular to the line segment joining (4, 3) and (−1, 1) if it cuts off an intercept −3 from y-axis.
Find the equations of the straight lines which cut off an intercept 5 from the y-axis and are equally inclined to the axes.
Show that the perpendicular bisectors of the sides of a triangle are concurrent.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (−1, 2).
Find the angles between the following pair of straight lines:
3x − y + 5 = 0 and x − 3y + 1 = 0
The medians AD and BE of a triangle with vertices A (0, b), B (0, 0) and C (a, 0) are perpendicular to each other, if
The equation of the line with slope −3/2 and which is concurrent with the lines 4x + 3y − 7 = 0 and 8x + 5y − 1 = 0 is
The equation of a line passing through the point (7, - 4) and perpendicular to the line passing through the points (2, 3) and (1 , - 2 ) is ______.
If x + y = k is normal to y2 = 12x, then k is ______.
Point of the curve y2 = 3(x – 2) at which the normal is parallel to the line 2y + 4x + 5 = 0 is ______.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
The equation of the straight line passing through the point (3, 2) and perpendicular to the line y = x is ______.
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is ______.
Equations of the lines through the point (3, 2) and making an angle of 45° with the line x – 2y = 3 are ______.
The points (3, 4) and (2, – 6) are situated on the ______ of the line 3x – 4y – 8 = 0.
If the vertices of a triangle have integral coordinates, then the triangle can not be equilateral.
The points A(– 2, 1), B(0, 5), C(– 1, 2) are collinear.
The line `x/a + y/b` = 1 moves in such a way that `1/a^2 + 1/b^2 = 1/c^2`, where c is a constant. The locus of the foot of the perpendicular from the origin on the given line is x2 + y2 = c2.
| Column C1 | Column C2 |
| (a) The coordinates of the points P and Q on the line x + 5y = 13 which are at a distance of 2 units from the line 12x – 5y + 26 = 0 are |
(i) (3, 1), (–7, 11) |
| (b) The coordinates of the point on the line x + y = 4, which are at a unit distance from the line 4x + 3y – 10 = 0 are |
(ii) `(- 1/3, 11/3), (4/3, 7/3)` |
| (c) The coordinates of the point on the line joining A (–2, 5) and B (3, 1) such that AP = PQ = QB are |
(iii) `(1, 12/5), (-3, 16/5)` |
The three straight lines ax + by = c, bx + cy = a and cx + ay = b are collinear, if ______.
