Advertisements
Advertisements
प्रश्न
Find the area of the region in the first quadrant enclosed by x-axis, line x = `sqrt3` y and the circle x2 + y2 = 4.
उत्तर
The area of the region bounded by the circle, `x^2 + y^2 = 4, x = sqrt3` and the x-axis is the area OAB.
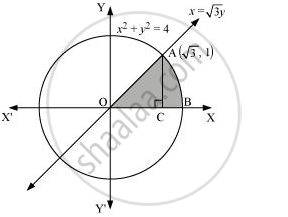
The point of intersection of the line and the circle in the first quadrant is .`(sqrt3,1)`
Area OAB = Area ΔOCA + Area ACB

Therefore, required area enclosed = 32 + π3 - 32 = π3 square units
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line `x = a/sqrt2`
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Find the area of the region bounded by the curve y2 = 4x and the line x = 3
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
Find the area of the smaller region bounded by the ellipse `x^2/9 + y^2/4` and the line `x/3 + y/2 = 1`
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Find the area enclosed between the parabola 4y = 3x2 and the straight line 3x - 2y + 12 = 0.
Find the area bounded by the circle x2 + y2 = 16 and the line `sqrt3 y = x` in the first quadrant, using integration.
Find the area of the smaller region bounded by the ellipse \[\frac{x^2}{9} + \frac{y^2}{4} = 1\] and the line \[\frac{x}{3} + \frac{y}{2} = 1 .\]
Draw a rough sketch and find the area bounded by the curve x2 = y and x + y = 2.
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
Find the area of the region bounded by the following curves, the X-axis and the given lines:
y = x2 + 1, x = 0, x = 3
Choose the correct alternative :
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is _______.
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
Fill in the blank :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _______.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
Choose the correct alternative:
Using the definite integration area of the circle x2 + y2 = 16 is ______
State whether the following statement is True or False:
The area bounded by the curve y = f(x) lies on the both sides of the X-axis is `|int_"a"^"b" "f"(x) "d"x| + |int_"b"^"c" "f"(x) "d"x|`
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
The area of the circle x2 + y2 = 16 is ______
Find area of the region bounded by the parabola x2 = 36y, y = 1 and y = 4, and the positive Y-axis
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
Area under the curve `y=sqrt(4x+1)` between x = 0 and x = 2 is ______.
The area bounded by the X-axis, the curve y = f(x) and the lines x = 1, x = b is equal to `sqrt("b"^2 + 1) - sqrt(2)` for all b > 1, then f(x) is ______.
Area of the region bounded by y= x4, x = 1, x = 5 and the X-axis is ______.
Area in first quadrant bounded by y = 4x2, x = 0, y = 1 and y = 4 is ______.
The area bounded by the x-axis and the curve y = 4x – x2 – 3 is ______.
Area bounded by y = sec2x, x = `π/6`, x = `π/3` and x-axis is ______.
The area bounded by the curve, y = –x, X-axis, x = 1 and x = 4 is ______.
If the area enclosed by y = f(x), X-axis, x = a, x = b and y = g(x), X-axis, x = a, x = b are equal, then f(x) = g(x).
The area enclosed by the parabola x2 = 4y and its latus rectum is `8/(6m)` sq units. Then the value of m is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
