Advertisements
Advertisements
प्रश्न
Find the distance from the eye at which a coin of 2 cm diameter should be held so as to conceal the full moon whose angular diameter is 31'.
उत्तर
Let PQ be the diameter of the coin and E be the eye of the observer.
Also, let the coin be kept at a distance r from the eye of the observer to hide the moon completely.
Now,
\[\theta = \frac{\text{Arc}}{\text{Radius}}\]
\[ \Rightarrow \frac{31}{60} \times \frac{\pi}{180} = \frac{2}{\text{Radius}}\]
\[ \Rightarrow\text{ Radius }= \frac{180 \times 60 \times 2 \times 7}{31 \times 22}\]
\[ = 221 . 7\text{ cm or }2 . 217 m\]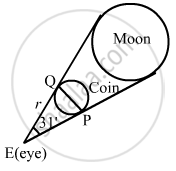
APPEARS IN
संबंधित प्रश्न
Find the radian measure corresponding to the following degree measure:
– 47° 30'
Find the radian measure corresponding to the following degree measure:
240°
Find the degree measure corresponding to the following radian measure (Use `pi = 22/7`)
-4
A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm
(Use `pi = 22/7`)
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
15 cm
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
21 cm
Find the degree measure corresponding to the following radian measure:
\[\frac{9\pi}{5}\]
Find the degree measure corresponding to the following radian measure:
\[- \frac{5\pi}{6}\]
Find the degree measure corresponding to the following radian measure:
(−3)c
Find the radian measure corresponding to the following degree measure:
300°
Find the radian measure corresponding to the following degree measure: 35°
Find the radian measure corresponding to the following degree measure: 135°
Find the radian measure corresponding to the following degree measure: −300°
One angle of a triangle \[\frac{2}{3}\] x grades and another is \[\frac{3}{2}\] x degrees while the third is \[\frac{\pi x}{75}\] radians. Express all the angles in degrees.
The angles of a triangle are in A.P. and the number of degrees in the least angle is to the number of degrees in the mean angle as 1 : 120. Find the angles in radians.
The angle in one regular polygon is to that in another as 3 : 2 and the number of sides in first is twice that in the second. Determine the number of sides of two polygons.
The radius of a circle is 30 cm. Find the length of an arc of this circle, if the length of the chord of the arc is 30 cm.
Find the diameter of the sun in km supposing that it subtends an angle of 32' at the eye of an observer. Given that the distance of the sun is 91 × 106 km.
If the angles of a triangle are in A.P., then the measures of one of the angles in radians is
At 3:40, the hour and minute hands of a clock are inclined at
If the arcs of the same length in two circles subtend angles 65° and 110° at the centre, than the ratio of the radii of the circles is
If OP makes 4 revolutions in one second, the angular velocity in radians per second is
A circular wire of radius 7 cm is cut and bent again into an arc of a circle of radius 12 cm. The angle subtended by the arc at the centre is
The radius of the circle whose arc of length 15 π cm makes an angle of \[\frac{3\pi}{4}\] radian at the centre is
If θ lies in the second quadrant, then show that `sqrt((1 - sin theta)/(1 + sin theta)) + sqrt((1 + sin theta)/(1 - sin theta))` = −2sec θ
Find the value of tan 9° – tan 27° – tan 63° + tan 81°
Prove that `(sec8 theta - 1)/(sec4 theta - 1) = (tan8 theta)/(tan2 theta)`
Which of the following is correct?
[Hint: 1 radian = `180^circ/pi = 57^circ30^'` approx]
State whether the statement is True or False? Also give justification.
The equality sinA + sin2A + sin3A = 3 holds for some real value of A.
