Advertisements
Advertisements
Question
Find the distance from the eye at which a coin of 2 cm diameter should be held so as to conceal the full moon whose angular diameter is 31'.
Solution
Let PQ be the diameter of the coin and E be the eye of the observer.
Also, let the coin be kept at a distance r from the eye of the observer to hide the moon completely.
Now,
\[\theta = \frac{\text{Arc}}{\text{Radius}}\]
\[ \Rightarrow \frac{31}{60} \times \frac{\pi}{180} = \frac{2}{\text{Radius}}\]
\[ \Rightarrow\text{ Radius }= \frac{180 \times 60 \times 2 \times 7}{31 \times 22}\]
\[ = 221 . 7\text{ cm or }2 . 217 m\]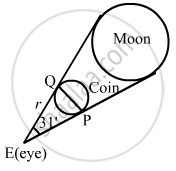
APPEARS IN
RELATED QUESTIONS
Find the radian measure corresponding to the following degree measure:
– 47° 30'
Find the radian measure corresponding to the following degree measure:
520°
Find the degree measure corresponding to the following radian measure (Use `pi = 22/7`)
-4
Find the degree measures corresponding to the following radian measures (Use `pi = 22/7`)
`(5pi)/3`
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
15 cm
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
21 cm
Find the degree measure corresponding to the following radian measure:
1c
Find the radian measure corresponding to the following degree measure:
300°
Find the radian measure corresponding to the following degree measure: 135°
Find the radian measure corresponding to the following degree measure: −300°
Find the radian measure corresponding to the following degree measure: 7° 30'
Find the radian measure corresponding to the following degree measure: 125° 30'
One angle of a triangle \[\frac{2}{3}\] x grades and another is \[\frac{3}{2}\] x degrees while the third is \[\frac{\pi x}{75}\] radians. Express all the angles in degrees.
Find the magnitude, in radians and degrees, of the interior angle of a regular octagon.
Find the magnitude, in radians and degrees, of the interior angle of a regular heptagon.
Let the angles of the quadrilateral be \[\left( a - 3d \right)^\circ, \left( a - d \right)^\circ, \left( a + d \right)^\circ \text{ and }\left( a + 3d \right)^\circ\]
We know: \[a - 3d + a - d + a + d + a - 2d = 360\]
\[ \Rightarrow 4a = 360\]
\[ \Rightarrow a = 90\]
We have:
Greatest angle = 120°
Now,
\[a + 3d = 120\]
\[ \Rightarrow 90 + 3d = 120\]
\[ \Rightarrow 3d = 30\]
\[ \Rightarrow d = 10\]
Hence,
\[\left( a - 3d \right)^\circ, \left( a - d \right)^\circ, \left( a + d \right)^\circ\text{ and }\left( a + 3d \right)^\circ\] are
Angles of the quadrilateral in radians =
The angles of a triangle are in A.P. and the number of degrees in the least angle is to the number of degrees in the mean angle as 1 : 120. Find the angles in radians.
The number of sides of two regular polygons are as 5 : 4 and the difference between their angles is 9°. Find the number of sides of the polygons.
A rail road curve is to be laid out on a circle. What radius should be used if the track is to change direction by 25° in a distance of 40 metres?
The radius of a circle is 30 cm. Find the length of an arc of this circle, if the length of the chord of the arc is 30 cm.
Find the diameter of the sun in km supposing that it subtends an angle of 32' at the eye of an observer. Given that the distance of the sun is 91 × 106 km.
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm.
If D, G and R denote respectively the number of degrees, grades and radians in an angle, the
If the angles of a triangle are in A.P., then the measures of one of the angles in radians is
At 3:40, the hour and minute hands of a clock are inclined at
If the arcs of the same length in two circles subtend angles 65° and 110° at the centre, than the ratio of the radii of the circles is
A circular wire of radius 7 cm is cut and bent again into an arc of a circle of radius 12 cm. The angle subtended by the arc at the centre is
The radius of the circle whose arc of length 15 π cm makes an angle of \[\frac{3\pi}{4}\] radian at the centre is
Find the value of `sqrt(3)` cosec 20° – sec 20°
If θ lies in the second quadrant, then show that `sqrt((1 - sin theta)/(1 + sin theta)) + sqrt((1 + sin theta)/(1 - sin theta))` = −2sec θ
Which of the following is correct?
[Hint: 1 radian = `180^circ/pi = 57^circ30^'` approx]
State whether the statement is True or False? Also give justification.
The equality sinA + sin2A + sin3A = 3 holds for some real value of A.
