Advertisements
Advertisements
प्रश्न
Find the distance from the eye at which a coin of 2 cm diameter should be held so as to conceal the full moon whose angular diameter is 31'.
उत्तर
Let PQ be the diameter of the coin and E be the eye of the observer.
Also, let the coin be kept at a distance r from the eye of the observer to hide the moon completely.
Now,
\[\theta = \frac{\text{Arc}}{\text{Radius}}\]
\[ \Rightarrow \frac{31}{60} \times \frac{\pi}{180} = \frac{2}{\text{Radius}}\]
\[ \Rightarrow\text{ Radius }= \frac{180 \times 60 \times 2 \times 7}{31 \times 22}\]
\[ = 221 . 7\text{ cm or }2 . 217 m\]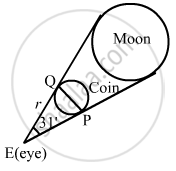
APPEARS IN
संबंधित प्रश्न
Find the radian measure corresponding to the following degree measure:
25°
Find the degree measure corresponding to the following radian measure `(use pi = 22/7)`
`11/16`
Find the degree measure corresponding to the following radian measure (Use `pi = 22/7`)
-4
Find the degree measures corresponding to the following radian measures (Use `pi = 22/7`)
`(5pi)/3`
Find the degree measure corresponding to the following radian measure (use `pi= 22/7`).
`(7pi)/6`
A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm
(Use `pi = 22/7`)
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
10 cm
Find the degree measure corresponding to the following radian measure:
\[\left( \frac{18\pi}{5} \right)\]
Find the degree measure corresponding to the following radian measure:
1c
Find the radian measure corresponding to the following degree measure: 35°
Find the radian measure corresponding to the following degree measure: 135°
Find the radian measure corresponding to the following degree measure: −300°
The difference between the two acute angles of a right-angled triangle is \[\frac{2\pi}{5}\] radians. Express the angles in degrees.
Find the magnitude, in radians and degrees, of the interior angle of a regular pentagon.
Find the magnitude, in radians and degrees, of the interior angle of a regular duodecagon.
Let the angles of the quadrilateral be \[\left( a - 3d \right)^\circ, \left( a - d \right)^\circ, \left( a + d \right)^\circ \text{ and }\left( a + 3d \right)^\circ\]
We know: \[a - 3d + a - d + a + d + a - 2d = 360\]
\[ \Rightarrow 4a = 360\]
\[ \Rightarrow a = 90\]
We have:
Greatest angle = 120°
Now,
\[a + 3d = 120\]
\[ \Rightarrow 90 + 3d = 120\]
\[ \Rightarrow 3d = 30\]
\[ \Rightarrow d = 10\]
Hence,
\[\left( a - 3d \right)^\circ, \left( a - d \right)^\circ, \left( a + d \right)^\circ\text{ and }\left( a + 3d \right)^\circ\] are
Angles of the quadrilateral in radians =
The number of sides of two regular polygons are as 5 : 4 and the difference between their angles is 9°. Find the number of sides of the polygons.
A rail road curve is to be laid out on a circle. What radius should be used if the track is to change direction by 25° in a distance of 40 metres?
Find the length which at a distance of 5280 m will subtend an angle of 1' at the eye.
The radius of a circle is 30 cm. Find the length of an arc of this circle, if the length of the chord of the arc is 30 cm.
A railway train is travelling on a circular curve of 1500 metres radius at the rate of 66 km/hr. Through what angle has it turned in 10 seconds?
If the arcs of the same length in two circles subtend angles 65° and 110° at the centre, find the ratio of their radii.
If the angles of a triangle are in A.P., then the measures of one of the angles in radians is
If the arcs of the same length in two circles subtend angles 65° and 110° at the centre, than the ratio of the radii of the circles is
A circular wire of radius 3 cm is cut and bent so as to lie along the circumference of a hoop whose radius is 48 cm. Find the angle in degrees which is subtended at the centre of hoop.
Find the value of tan 9° – tan 27° – tan 63° + tan 81°
“The inequality `2^sintheta + 2^costheta ≥ 2^(1/sqrt(2))` holds for all real values of θ”
The value of cos1° cos2° cos3° ... cos179° is ______.
Which of the following is correct?
[Hint: 1 radian = `180^circ/pi = 57^circ30^'` approx]
State whether the statement is True or False? Also give justification.
The equality sinA + sin2A + sin3A = 3 holds for some real value of A.
State whether the statement is True or False? Also give justification.
One value of θ which satisfies the equation sin4θ - 2sin2θ - 1 lies between 0 and 2π.
