Advertisements
Advertisements
प्रश्न
Four balls are to be drawn without replacement from a box containing 8 red and 4 white balls. If X denotes the number of red ball drawn, find the probability distribution of X.
उत्तर
Since 4 balls have to be drawn, therefore, X can take the values 0, 1, 2, 3, 4.
P(X = 0) = P(no red ball) = P(4 white balls)
= `(""^4"C"_4)/(""^12"C"_4) = 1/495`
P(X = 1) = P(1 red ball and 3 white balls)
= `(""^8"C"_1 xx ""^4"C"_3)/(""^12"C"_4) = 32/495`
P(X = 2) = P(2 red balls and 2 white balls)
= `(""^8"C"_2 xx ""^4"C"_2)/(""^12"C"_4) = 168/495`
P(X = 3) = P(3 red balls and 1 white ball)
= `(""^8"C"_3 xx ""^4"C"_1)/(""^12"C"_4) = 224/495`
P(X = 4) = P(4 red balls)
= `(""^8"C"_4)/(""^12"C"_4) = 70/495`
Thus the following is the required probability distribution of X
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | `1/495` | `32/495` | `168/195` | `224/495` | `70/495` |
APPEARS IN
संबंधित प्रश्न
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| Z | 3 | 2 | 1 | 0 | -1 |
| P(Z) | 0.3 | 0.2 | 0.4 | 0.1 | 0.05 |
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denotes the larger of the two numbers obtained. Find E(X).
An urn contains 25 balls of which 10 balls bear a mark ‘X’ and the remaining 15 bear a mark ‘Y’. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear ‘X’ mark.
(ii) not more than 2 will bear ‘Y’ mark.
(iii) at least one ball will bear ‘Y’ mark
(iv) the number of balls with ‘X’ mark and ‘Y’ mark will be equal.
There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean 'and variance of X.
Two numbers are selected at random (without replacement) from positive integers 2, 3, 4, 5, 6 and 7. Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X.
Find the probability distribution of the number of heads, when three coins are tossed.
Two cards are drawn simultaneously from a well-shuffled deck of 52 cards. Find the probability distribution of the number of successes, when getting a spade is considered a success.
A fair die is tossed twice. If the number appearing on the top is less than 3, it is a success. Find the probability distribution of number of successes.
The probability distribution of a random variable X is given below:
| x | 0 | 1 | 2 | 3 |
| P(X) | k |
\[\frac{k}{2}\]
|
\[\frac{k}{4}\]
|
\[\frac{k}{8}\]
|
Determine P(X ≤ 2) and P(X > 2) .
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | k2 | 2k2 | k |
Determine the mean of the distribution.
Three cards are drawn at random (without replacement) from a well shuffled pack of 52 cards. Find the probability distribution of number of red cards. Hence, find the mean of the distribution .
The expenditure Ec of a person with income I is given by Ec = (0.000035) I2 + (0. 045) I. Find marginal propensity to consume (MPC) and average propensity to consume (APC) when I = 5000.
If X ∼ N (4,25), then find P(x ≤ 4)
The probability that a bomb dropped from an aeroplane will strike a target is `1/5`, If four bombs are dropped, find the probability that :
(a) exactly two will strike the target,
(b) at least one will strike the target.
Find expected value and variance of X, where X is number obtained on uppermost face when a fair die is thrown.
The p.d.f. of r.v. of X is given by
f (x) = `k /sqrtx` , for 0 < x < 4 and = 0, otherwise. Determine k .
Determine c.d.f. of X and hence P (X ≤ 2) and P(X ≤ 1).
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 |
| P(x) | 0.4 | 0.4 | 0.2 |
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 |
| P(x) | 0.3 | 0.4 | 0.2 |
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of X ≤ 1
Solve the following problem :
Following is the probability distribution of a r.v.X.
| x | – 3 | – 2 | –1 | 0 | 1 | 2 | 3 |
| P(X = x) | 0.05 | 0.1 | 0.15 | 0.20 | 0.25 | 0.15 | 0.1 |
Find the probability that X is even.
Solve the following problem :
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics.
Calculate the probabilities of obtaining an answer yes from all of the selected students.
Let X be a discrete random variable. The probability distribution of X is given below:
| X | 30 | 10 | – 10 |
| P(X) | `1/5` | `3/10` | `1/2` |
Then E(X) is equal to ______.
A discrete random variable X has the probability distribution given as below:
| X | 0.5 | 1 | 1.5 | 2 |
| P(X) | k | k2 | 2k2 | k |
Determine the mean of the distribution.
The random variable X can take only the values 0, 1, 2. Given that P(X = 0) = P(X = 1) = p and that E(X2) = E[X], find the value of p
If the p.m.f of a r. v. X is
P(x) = `c/x^3`, for x = 1, 2, 3
= 0, otherwise
then E(X) = ______.
Find the mean number of defective items in a sample of two items drawn one-by-one without replacement from an urn containing 6 items, which include 2 defective items. Assume that the items are identical in shape and size.
Two balls are drawn at random one by one with replacement from an urn containing equal number of red balls and green balls. Find the probability distribution of number of red balls. Also, find the mean of the random variable.
Two numbers are selected from first six even natural numbers at random without replacement. If X denotes the greater of two numbers selected, find the probability distribution of X.
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
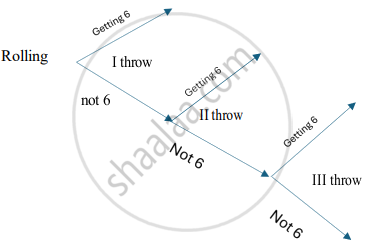
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
