Advertisements
Advertisements
प्रश्न
State whether the following statement is True or False:
The graphical solution set of the inequations 0 ≤ y, x ≥ 0 lies in second quadrant
पर्याय
True
False
उत्तर
False
APPEARS IN
संबंधित प्रश्न
A farmer has a 100 acre farm. He can sell the tomatoes, lettuce, or radishes he can raise. The price he can obtain is Rs 1 per kilogram for tomatoes, Rs 0.75 a head for lettuce and Rs 2 per kilogram for radishes. The average yield per acre is 2000 kgs for radishes, 3000 heads of lettuce and 1000 kilograms of radishes. Fertilizer is available at Rs 0.50 per kg and the amount required per acre is 100 kgs each for tomatoes and lettuce and 50 kilograms for radishes. Labour required for sowing, cultivating and harvesting per acre is 5 man-days for tomatoes and radishes and 6 man-days for lettuce. A total of 400 man-days of labour are available at Rs 20 per man-day. Formulate this problem as a LPP to maximize the farmer's total profit.
Solve the following L.P.P. by graphical method :
Maximize: Z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of Z.
Solve the following L.P.P. by graphical method :
Minimize : Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Choose the correct alternative :
The maximum value of z = 10x + 6y, subjected to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, y ≥ 0 is.
Choose the correct alternative :
The point at which the maximum value of z = x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
Solve the following problem :
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components, a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufacture per month to maximize profit? How much is the maximum profit?
Choose the correct alternative:
The corner points of the feasible region are (0, 3), (3, 0), (8, 0), `(12/5, 38/5)` and (0, 10), then the point of maximum Z = 6x + 4y = 48 is at
State whether the following statement is True or False:
The maximum value of Z = 5x + 3y subjected to constraints 3x + y ≤ 12, 2x + 3y ≤ 18, 0 ≤ x, y is 20
State whether the following statement is True or False:
If LPP has two optimal solutions, then the LPP has infinitely many solutions
State whether the following statement is True or False:
If the corner points of the feasible region are `(0, 7/3)`, (2, 1), (3, 0) and (0, 0), then the maximum value of Z = 4x + 5y is 12
A dealer deals in two products X and Y. He has ₹ 1,00,000/- to invest and space to store 80 pieces. Product X costs ₹ 2500/- and product Y costs ₹ 1000/- per unit. He can sell the items X and Y at respective profits of ₹ 300 and ₹ 90. Construct the LPP and find the number of units of each product to be purchased to maximize its profit
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
Maximize Z = 5x + 10y subject to constraints
x + 2y ≤ 10, 3x + y ≤ 12, x ≥ 0, y ≥ 0
Amartya wants to invest ₹ 45,000 in Indira Vikas Patra (IVP) and in Public Provident fund (PPF). He wants to invest at least ₹ 10,000 in PPF and at least ₹ 5000 in IVP. If the rate of interest on PPF is 8% per annum and that on IVP is 7% per annum. Formulate the above problem as LPP to determine maximum yearly income.
Solution: Let x be the amount (in ₹) invested in IVP and y be the amount (in ₹) invested in PPF.
x ≥ 0, y ≥ 0
As per the given condition, x + y ______ 45000
He wants to invest at least ₹ 10,000 in PPF.
∴ y ______ 10000
Amartya wants to invest at least ₹ 5000 in IVP.
∴ x ______ 5000
Total interest (Z) = ______
The formulated LPP is
Maximize Z = ______ subject to
______
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.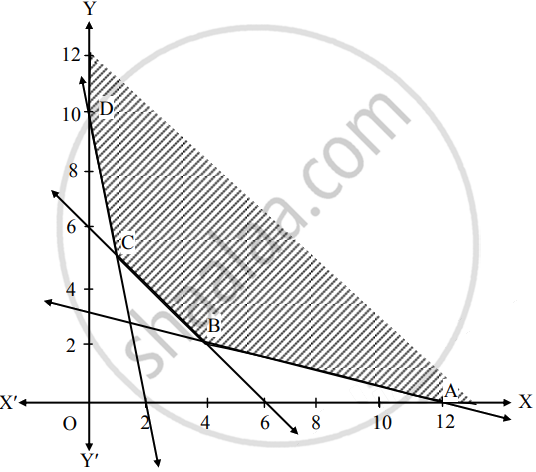
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
