Advertisements
Advertisements
प्रश्न
The refractive index of a material changes by 0.014 as the colour of the light changes from red to violet. A rectangular slab of height 2.00 cm made of this material is placed on a newspaper. When viewed normally in yellow light, the letters appear 1.32 cm below the top surface of the slab. Calculate the dispersive power of the material.
उत्तर
Given:-
Difference in the refractive indices of violet and red lights = 0.014
Let μv and μr be the refractive indices of violet and red colours.
Thus, we have:-
μv − μr = 0.014
Now,
Real depth of the newspaper = 2.00 cm
Apparent depth of the newspaper = 1.32 cm
\[\text{Refractive index }= \frac{\text{Real depth}}{\text{Apparent depth}}\]
Refractive index for yellow light \[\left( \mu_y \right)\] is given by
\[ \mu_y = \frac{2 . 00}{1 . 32} = 1 . 515\]
Also,
Dispersive power, \[\omega = \frac{\mu_v - \mu_r}{\mu_y - 1}\]
\[= \frac{0 . 014}{1 . 515 - 1}\]
Or, \[\omega = \frac{0 . 014}{0 . 515} = 0 . 027\]
Thus, the dispersive power of the material is 0.027.
APPEARS IN
संबंधित प्रश्न
A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
Determine the value of the angle of incidence for a ray of light travelling from a medium of refractive index \[\mu_1 = \sqrt{2}\] into the medium of refractive index \[\mu_2 = 1\] so that it just grazes along the surface of separation.
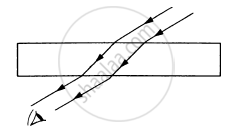
A narrow beam of light passes through a slab obliquely and is then received by an eye following figure. The index of refraction of the material in the slab fluctuates slowly with time. How will it appear to the eye? The twinkling of stars has a similar explanation.
If the light moving in a straight line bends by a small but fixed angle, it may be a case of
(a) reflection
(b) refraction
(c) diffraction
(d) dispersion.
A pole of length 1.00 m stands half dipped in a swimming pool with water level 50.0 cm higher than the bed. The refractive index of water is 1.33 and sunlight is coming at an angle of 45° with the vertical. Find the length of the shadow of the pole on the bed.
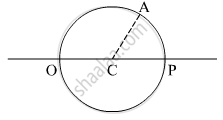
Consider the situation in figure. The bottom of the pot is a reflecting plane mirror, S is a small fish and T is a human eye. Refractive index of water is μ. (a) At what distance(s) from itself will the fish see the image(s) of the eye? (b) At what distance(s) from itself will the eye see the image(s) of the fish.

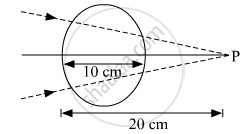
A converging beam of light traveling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1⋅5 is introduced in between the path of the beam, calculate the new position of, the image. Also, draw the ray diagram for the image formed.
Answer the following question.
Define absolute refractive index and relative refractive index. Explain in brief with an illustration for each.
What is relative refractive index?
Why do stars twinkle?
Obtain the equation for critical angle.
Obtain the equation for radius of illumination (or) Snell’s window.
The optical density of turpentine is higher than that of water while its mass density is lower. Figure shows a layer of turpentine floating over water in a container. For which one of the four rays incident on turpentine in figure, the path shown is correct?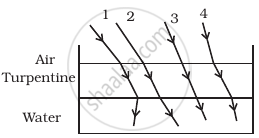
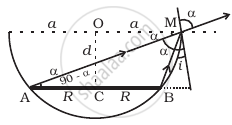
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
Show that for a material with refractive index `µ ≥ sqrt(2)`, light incident at any angle shall be guided along a length perpendicular to the incident face.
A beam of light travels from air into a medium. Its speed and wavelength in the medium are 1.5 × 108 ms-1 and 230 nm respectively. The wavelength of light in the air will be ______.
