Advertisements
Advertisements
प्रश्न
Write the length of the chord of the parabola y2 = 4ax which passes through the vertex and is inclined to the axis at \[\frac{\pi}{4}\]
उत्तर
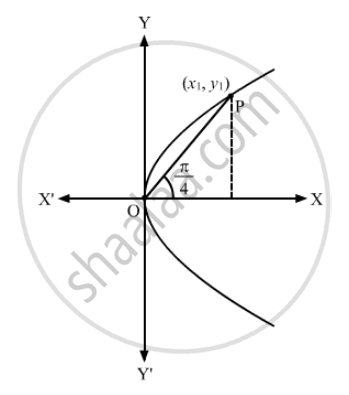 Let OP be the chord.
Let OP be the chord.
Let the coordinates of P be \[\left( x_1 , y_1 \right)\]
From the figure, we have:
\[O P^2 = {x_1}^2 + {y_1}^2\]
And, \[\tan\frac{\pi}{4} = \frac{y_1}{x_1}\]
\[\Rightarrow x_1 = y_1\] (2)
Also, \[\left( x_1 , y_1 \right)\] lies on the parabola.
∴ \[{y_1}^2 = 4a x_1 (3)
Using (2) and (3), we get:
\[{x_1}^2 = 4a x_1 \Rightarrow x_1 = 4a\] ...(4)
∴ From (4), (1) and (2), we have:
\[O P^2 = \left( 4a \right)^2 + \left( 4a \right)^2 = 32 a^2 \]
\[ \Rightarrow OP = 4\sqrt{2}a\]
Therefore, the length of the chord is \[4\sqrt{2}a \text{ units }\]
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/36 + y^2/16 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/4 + y^2/25 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/25 + y^2/100 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
`x^2/49 + y^2/36 = 1`
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
36x2 + 4y2 = 144
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
4x2 + 9y2 = 36
A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.
Find the vertex, focus, axis, directrix and latus-rectum of the following parabolas
y2 − 4y − 3x + 1 = 0
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 − 4y + 4x = 0
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 + 4x + 4y − 3 = 0
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
4 (y − 1)2 = − 7 (x − 3)
Find the vertex, focus, axis, directrix and latus-rectum of the following parabola
y2 = 5x − 4y − 9
Write the distance between the vertex and focus of the parabola y2 + 6y + 2x + 5 = 0.
Write the coordinates of the vertex of the parabola whose focus is at (−2, 1) and directrix is the line x + y − 3 = 0.
If the coordinates of the vertex and focus of a parabola are (−1, 1) and (2, 3) respectively, then write the equation of its directrix.
The vertex of the parabola (y − 2)2 = 16 (x − 1) is
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
x2 + 2y2 − 2x + 12y + 10 = 0
Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:
x2 + 4y2 − 2x = 0
A rod of length 12 m moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with x-axis.
Find the equation of the set of all points whose distances from (0, 4) are\[\frac{2}{3}\] of their distances from the line y = 9.
If the lengths of semi-major and semi-minor axes of an ellipse are 2 and \[\sqrt{3}\] and their corresponding equations are y − 5 = 0 and x + 3 = 0, then write the equation of the ellipse.
Write the eccentricity of the ellipse 9x2 + 5y2 − 18x − 2y − 16 = 0.
If the minor axis of an ellipse subtends an equilateral triangle with vertex at one end of major axis, then write the eccentricity of the ellipse.
The equation of the circle having centre (1, –2) and passing through the point of intersection of the lines 3x + y = 14 and 2x + 5y = 18 is ______.
The equation of the ellipse whose centre is at the origin and the x-axis, the major axis, which passes through the points (–3, 1) and (2, –2) is ______.
The equation of the circle which passes through the point (4, 5) and has its centre at (2, 2) is ______.
If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
The shortest distance from the point (2, –7) to the circle x2 + y2 – 14x – 10y – 151 = 0 is equal to 5.
