Advertisements
Advertisements
प्रश्न
Write the mathematical expression of the First Law of Thermodynamics for Isothermal Process
उत्तर
Temperature is constant in such a process; internal energy is constant.
Hence, ∆U = 0
For isothermal process
0 = Q + W or W = - Q
APPEARS IN
संबंधित प्रश्न
An electric heater supplies heat to a system at a rate of 100W. If the system performs work at a rate of 75 Joules per second. At what rate is the internal energy increasing?
Write the mathematical expression of the First Law of Thermodynamics for the Isobaric process.
The first law of thermodynamics is a statement of ____________ .
Refer to figure. Let ∆U1 and ∆U2 be the change in internal energy in processes A and B respectively, ∆Q be the net heat given to the system in process A + B and ∆W be the net work done by the system in the process A + B.

(a) ∆U1 + ∆U2 = 0
(b) ∆U1 − ∆U2 = 0
(c) ∆Q − ∆W = 0
(d) ∆Q + ∆W = 0
A thermally insulated, closed copper vessel contains water at 15°C. When the vessel is shaken vigorously for 15 minutes, the temperature rises to 17°C. The mass of the vessel is 100 g and that of the water is 200 g. The specific heat capacities of copper and water are 420 J kg−1 K−1 and 4200 J kg−1 K−1 respectively. Neglect any thermal expansion. (a) How much heat is transferred to the liquid-vessel system? (b) How much work has been done on this system? (c) How much is the increase in internal energy of the system?
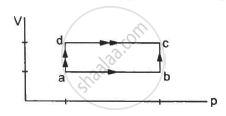
When a system is taken through the process abc shown in figure, 80 J of heat is absorbed by the system and 30 J of work is done by it. If the system does 10 J of work during the process adc, how much heat flows into it during the process?
The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10 cm. Find the increase in the internal energy of the gas. The area of cross section of the cylinder = 4 cm2 and the atmospheric pressure = 100 kPa.
The process, in which no heat enters or leaves the system, is termed as ____________.
Change in internal energy, when 4 KJ of work is done on the system and 1 KJ heat is given out by the system, is:
If an average person jogs, hse produces 14.5 × 103 cal/min. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming 1 kg requires 580 × 103 cal for evaparation) is ______.
An ideal gas undergoes cyclic process ABCDA as shown in given P-V diagram (figure). The amount of work done by the gas is ______.

An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
- dU = 0
- dQ= 0
- dQ = dU
- dQ = dW
Is it possible to increase the temperature of a gas without adding heat to it? Explain.
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
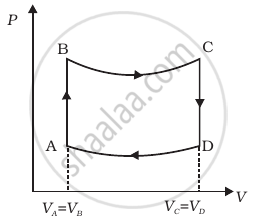
- In which part of the cycle heat is supplied to the engine from outside?
- In which part of the cycle heat is being given to the surrounding by the engine?
- What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
- What is the efficiency of the engine?
(γ = `5/3` for the gas), (Cv = `3/2` R for one mole)
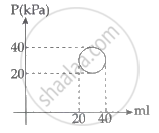
In the reported figure, heat energy absorbed by a system in going through a cyclic process is ______ πJ.
200g water is heated from 40°C to 60°C. Ignoring the slight expansion of water, the change in its internal energy is close to ______.
(Given specific heat of water = 4184 J/kgK)
The first law of thermodynamics for isothermal process is ______.
One mole of an ideal gas is allowed to expand reversibly and adiabatically from a temperature of 27°C. If the work done during the process is 3 kJ, the final temperature will be equal to ______.
(Cv = 20 JK−1)
The V cc volume of gas having `γ = 5/2` is suddenly compressed to `(V/4)` cc. The initial pressure of the gas is p. The final pressure of the gas will be ______.
What work will be done, when 3 moles of an ideal gas are compressed to half the initial volume at a constant temperature of 300 K?
An ideal gas having pressure p, volume V and temperature T undergoes a thermodynamic process in which dW = 0 and dQ < 0. Then, for the gas ______.
Derive an expression for the work done during an isothermal process.
104 J of work is done on a certain volume of a gas. If the gas releases 125 kJ of heat, calculate the change in internal energy of the gas.
If the adiabatic ratio for a gas is 5/3, find the molar specific heat capacity of the gas at (i) constant volume (ii) constant pressure.
For an isothermal and reversible expansion of 0.5 mol of an ideal gas Wmax is - 3.918 kJ. The value of ΔU is ______.
Using the first law of thermodynamics, show that for an ideal gas, the difference between the molar specific heat capacities at constant pressure and at constant volume is equal to the molar gas constant R.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
Define the isothermal process.
