Advertisements
Advertisements
प्रश्न
Write the order of the differential equation of the family of circles touching X-axis at the origin.
उत्तर
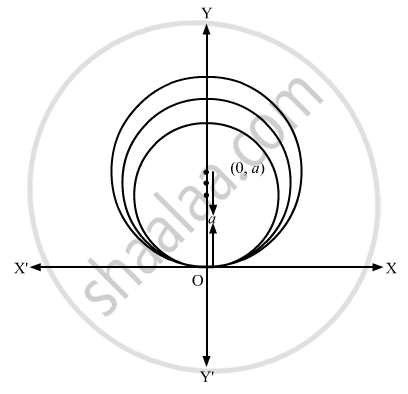
The equation of the family of circles touching x-axis at the origin is \[\left( x - 0 \right)^2 + \left( y - a \right)^2 = a^2 \]
\[ x^2 + y^2 - 2ay = 0 . . . . . \left( 1 \right)\]
Here, a is the parameter .
Since this equation contains only one arbitary constant, we differentiate it only once .
Differentiating with respect to x, we get
\[2x + 2y\frac{dy}{dx} - 2a\frac{dy}{dx} = 0\]
\[a = \frac{x + y\left( \frac{dy}{dx} \right)}{\frac{dy}{dx}} . . . . . \left( 2 \right)\]
Putting the value of a from (2) in (1), we get
\[ x^2 + y^2 = 2y\left\{ \frac{x + y\left( \frac{dy}{dx} \right)}{\frac{dy}{dx}} \right\}\]
\[\left( x^2 - y^2 \right)\frac{dy}{dx} = 2xy\]
So, this is the required differential equation .
Here, order of the differential equation is 1 .
APPEARS IN
संबंधित प्रश्न
Determine the order and degree (if defined) of the differential equation:
y' + 5y = 0
Determine the order and degree (if defined) of the differential equation:
( y′′′) + (y″)3 + (y′)4 + y5 = 0
For the given below, verify that the given function (implicit or explicit) is a solution to the corresponding differential equation.
`y = e^x (acos x + b sin x) : (d^2y)/(dx^2) - 2 dy/dx + 2y = 0`
Write the order of the differential equation
\[1 + \left( \frac{dy}{dx} \right)^2 = 7 \left( \frac{d^2 y}{d x^2} \right)^3\]
Write the degree of the differential equation
\[\frac{d^2 y}{d x^2} + x \left( \frac{dy}{dx} \right)^2 = 2 x^2 \log \left( \frac{d^2 y}{d x^2} \right)\]
Write the degree of the differential equation x \[\left( \frac{d^2 y}{d x^2} \right)^3 + y \left( \frac{dy}{dx} \right)^4 + x^3 = 0\]
Write the degree of the differential equation \[\left( 1 + \frac{dy}{dx} \right)^3 = \left( \frac{d^2 y}{d x^2} \right)^2\]
Find the sum of the order and degree of the differential equation
\[y = x \left( \frac{dy}{dx} \right)^3 + \frac{d^2 y}{d x^2}\]
The degree of the differential equation \[\left( \frac{d^2 y}{d x^2} \right)^3 + \left( \frac{dy}{dx} \right)^2 + \sin\left( \frac{dy}{dx} \right) + 1 = 0\], is
Determine the order and degree (if defined) of the following differential equation:-
(y"')2 + (y")3 + (y')4 + y5 = 0
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
y = cos x + C y' + sin x = 0
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
`y=sqrt(1+x^2)` `y'=(xy)/(1+x^2)`
Write the order and the degree of the following differential equation: `"x"^3 ((d^2"y")/(d"x"^2))^2 + "x" ((d"y")/(d"x"))^4 = 0`
Determine the order and degree of the following differential equation:
`root(3)(1 +("dy"/"dx")^2) = ("d"^2"y")/"dx"^2`
Determine the order and degree of the following differential equation:
`(dy)/(dx) = (2sin x + 3)/(dy/dx)`
Determine the order and degree of the following differential equation:
`(("d"^3"y")/"dx"^3)^(1/2) - ("dy"/"dx")^(1/3) = 20`
Determine the order and degree of the following differential equation:
`("d"^4"y")/"dx"^4 + sin ("dy"/"dx") = 0`
Determine the order and degree of the following differential equations.
`(d^4y)/dx^4 + [1+(dy/dx)^2]^3 = 0`
Determine the order and degree of the following differential equations.
`sqrt(1+1/(dy/dx)^2) = (dy/dx)^(3/2)`
Choose the correct alternative.
The order and degree of `[ 1+ (dy/dx)^3]^(2/3) = 8 (d^3y)/dx^3` are respectively.
Choose the correct alternative:
The order and degree of `(1 + (("d"y)/("d"x))^3)^(2/3) = 8 ("d"^3y)/("d"x^3)` are respectively
State whether the following statement is True or False:
Order and degree of differential equation `x ("d"^3y)/("d"x^3) + 6(("d"^2y)/("d"x^2))^2 + y` = 0 is (2, 2)
Degree of the given differential equation
`(("d"^3"y")/"dx"^2)^2 = (1 + "dy"/"dx")^(1/3)` is
The differential equation `x((d^2y)/dx^2)^3 + ((d^3y)/dx^3)^2y = x^2` is of ______
The degree of the differential equation `1/2 ("d"^3"y")/"dx"^3 = {1 + (("d"^2"y")/"dx"^2)}^(5/3)` is ______.
Order of the differential equation representing the family of ellipses having centre at origin and foci on x-axis is two.
The degree of the differential equation `sqrt(1 + (("d"y)/("d"x))^2)` = x is ______.
Write the degree of the differential equation (y''')2 + 3(y") + 3xy' + 5y = 0
The order and degree of the differential equation `[1 + ((dy)/(dx))^3]^(2/3) = 8((d^3y)/(dx^3))` are respectively ______.
The degree and order of the differential equation `[1 + (dy/dx)^3]^(7/3) = 7((d^2y)/(dx^2))` respectively are ______.
The degree of the differential equation `((d^2y)/dx^2)^2 + (dy/dx)^3` = ax is 3.
Degree of the differential equation `sinx + cos(dy/dx)` = y2 is ______.
Find the order and degree of the differential equation
`sqrt(1 + 1/(dy/dx)^2) = ((d^2y)/(dx^2))^(3/2)`
