Advertisements
Advertisements
Question
Write the order of the differential equation of the family of circles touching X-axis at the origin.
Solution
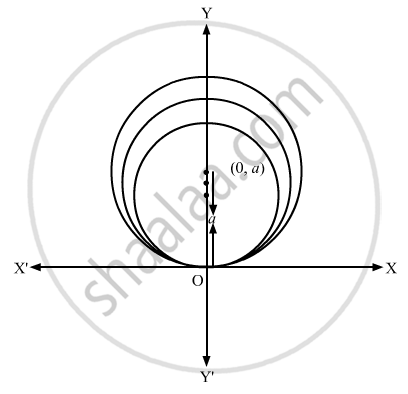
The equation of the family of circles touching x-axis at the origin is \[\left( x - 0 \right)^2 + \left( y - a \right)^2 = a^2 \]
\[ x^2 + y^2 - 2ay = 0 . . . . . \left( 1 \right)\]
Here, a is the parameter .
Since this equation contains only one arbitary constant, we differentiate it only once .
Differentiating with respect to x, we get
\[2x + 2y\frac{dy}{dx} - 2a\frac{dy}{dx} = 0\]
\[a = \frac{x + y\left( \frac{dy}{dx} \right)}{\frac{dy}{dx}} . . . . . \left( 2 \right)\]
Putting the value of a from (2) in (1), we get
\[ x^2 + y^2 = 2y\left\{ \frac{x + y\left( \frac{dy}{dx} \right)}{\frac{dy}{dx}} \right\}\]
\[\left( x^2 - y^2 \right)\frac{dy}{dx} = 2xy\]
So, this is the required differential equation .
Here, order of the differential equation is 1 .
APPEARS IN
RELATED QUESTIONS
Determine the order and degree (if defined) of the differential equation:
`(d^2y)/(dx^2)` = cos 3x + sin 3x
Define order of a differential equation.
Define degree of a differential equation.
Write the order of the differential equation
\[1 + \left( \frac{dy}{dx} \right)^2 = 7 \left( \frac{d^2 y}{d x^2} \right)^3\]
Write the degree of the differential equation
\[\frac{d^2 y}{d x^2} + x \left( \frac{dy}{dx} \right)^2 = 2 x^2 \log \left( \frac{d^2 y}{d x^2} \right)\]
Write the degree of the differential equation \[\left( 1 + \frac{dy}{dx} \right)^3 = \left( \frac{d^2 y}{d x^2} \right)^2\]
Write the degree of the differential equation \[\frac{d^2 y}{d x^2} + 3 \left( \frac{dy}{dx} \right)^2 = x^2 \log\left( \frac{d^2 y}{d x^2} \right)\]
The order of the differential equation whose general solution is given by y = c1 cos (2x + c2) − (c3 + c4) ax + c5 + c6 sin (x − c7) is
Write the sum of the order and degree of the differential equation
\[\left( \frac{d^2 y}{{dx}^2} \right)^2 + \left( \frac{dy}{dx} \right)^3 + x^4 = 0 .\]
Determine the order and degree (if defined) of the following differential equation:-
y"' + 2y" + y' = 0
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
y = cos x + C y' + sin x = 0
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
`y=sqrt(1+x^2)` `y'=(xy)/(1+x^2)`
Determine the order and degree of the following differential equation:
`("d"^2"y")/"dx"^2 + "x"("dy"/"dx")` + y = 2 sin x
Determine the order and degree of the following differential equation:
`root(3)(1 +("dy"/"dx")^2) = ("d"^2"y")/"dx"^2`
Determine the order and degree of the following differential equation:
`(dy)/(dx) = (2sin x + 3)/(dy/dx)`
Choose the correct option from the given alternatives:
The order and degree of the differential equation `sqrt(1 + ("dy"/"dx")^2) = (("d"^2"y")/"dx"^2)^(3/2)` are respectively.
Determine the order and degree of the following differential equations.
`((d^2y)/(dx^2))^2 + ((dy)/(dx))^2 =a^x `
Choose the correct alternative.
The order and degree of `[ 1+ (dy/dx)^3]^(2/3) = 8 (d^3y)/dx^3` are respectively.
Order and degree of a differential equation are always positive integers.
The order and degree of `((dy)/(dx))^3 - (d^3y)/(dx^3) + ye^x` = 0 are ______.
Order and degree of differential equation are always ______ integers
The power of highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called ______ of the differential equation
State whether the following statement is True or False:
Order and degree of differential equation `x ("d"^3y)/("d"x^3) + 6(("d"^2y)/("d"x^2))^2 + y` = 0 is (2, 2)
The degree of the differential equation `("d"^4"y")/"dx"^4 + sqrt(1 + ("dy"/"dx")^4)` = 0 is
The order and degree of the differential equation `(dy/dx)^3 + ((d^3y)/dx^3) + xy = 0` are respectively ______
If m and n are the order and degree of the differential equation `((d^3y)/(dx^3))^6+5((d^3y)/(dx^3))^4/((d^4y)/(dx^4))+(d^4y)/(dx^4)=x^3-1,` then ______.
The degree of the differential equation `("d"^2y)/("d"x^2) + 3("dy"/"dx")^2 = x^2 log(("d"^2y)/("d"x^2))` is ______.
Order of the differential equation representing the family of parabolas y2 = 4ax is ______.
The degree of the differential equation `(("d"^2y)/("d"x^2))^2 + (("d"y)/("d"x))^2 = xsin(("d"y)/("d"x))` is ______.
The degree of the differential equation `sqrt(1 + (("d"y)/("d"x))^2)` = x is ______.
The order of differential equation `2x^2 (d^2y)/(dx^2) - 3 (dy)/(dx) + y` = 0 is
The order and degree of the differential equation `[1 + ((dy)/(dx))^3]^(2/3) = 8((d^3y)/(dx^3))` are respectively ______.
The order of the differential equation of all parabolas, whose latus rectum is 4a and axis parallel to the x-axis, is ______.
If `(a + bx)e^(y/x)` = x then prove that `x(d^2y)/(dx^2) = (a/(a + bx))^2`.
The degree of the differential equation `[1 + (dy/dx)^2]^3 = ((d^2y)/(dx^2))^2` is ______.
