Advertisements
Advertisements
प्रश्न
Write the order of the differential equation of the family of circles touching X-axis at the origin.
उत्तर
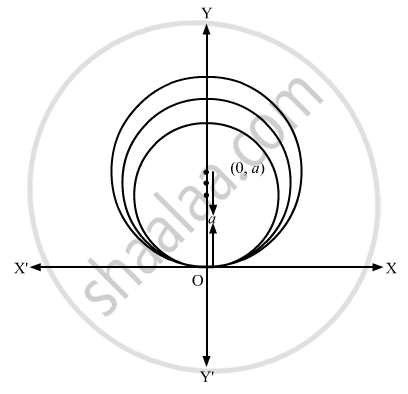
The equation of the family of circles touching x-axis at the origin is \[\left( x - 0 \right)^2 + \left( y - a \right)^2 = a^2 \]
\[ x^2 + y^2 - 2ay = 0 . . . . . \left( 1 \right)\]
Here, a is the parameter .
Since this equation contains only one arbitary constant, we differentiate it only once .
Differentiating with respect to x, we get
\[2x + 2y\frac{dy}{dx} - 2a\frac{dy}{dx} = 0\]
\[a = \frac{x + y\left( \frac{dy}{dx} \right)}{\frac{dy}{dx}} . . . . . \left( 2 \right)\]
Putting the value of a from (2) in (1), we get
\[ x^2 + y^2 = 2y\left\{ \frac{x + y\left( \frac{dy}{dx} \right)}{\frac{dy}{dx}} \right\}\]
\[\left( x^2 - y^2 \right)\frac{dy}{dx} = 2xy\]
So, this is the required differential equation .
Here, order of the differential equation is 1 .
APPEARS IN
संबंधित प्रश्न
Determine the order and degree (if defined) of the differential equation:
`(d^4y)/(dx^4) + sin(y^("')) = 0`
Determine the order and degree (if defined) of the differential equation:
y' + 5y = 0
Determine the order and degree (if defined) of the differential equation:
`(d^2y)/(dx^2)^2 + cos(dy/dx) = 0`
Determine the order and degree (if defined) of the differential equation:
y′′′ + 2y″ + y′ = 0
Define degree of a differential equation.
Write the degree of the differential equation \[x^3 \left( \frac{d^2 y}{d x^2} \right)^2 + x \left( \frac{dy}{dx} \right)^4 = 0\]
Write the degree of the differential equation \[\frac{d^2 y}{d x^2} + 3 \left( \frac{dy}{dx} \right)^2 = x^2 \log\left( \frac{d^2 y}{d x^2} \right)\]
Write the degree of the differential equation \[\left( \frac{d^2 y}{d x^2} \right)^2 + \left( \frac{dy}{dx} \right)^2 = x\sin\left( \frac{dy}{dx} \right)\]
The degree of the differential equation \[\left( \frac{d^2 y}{d x^2} \right)^3 + \left( \frac{dy}{dx} \right)^2 + \sin\left( \frac{dy}{dx} \right) + 1 = 0\], is
The order of the differential equation \[2 x^2 \frac{d^2 y}{d x^2} - 3\frac{dy}{dx} + y = 0\], is
Determine the order and degree (if defined) of the following differential equation:-
(y"')2 + (y")3 + (y')4 + y5 = 0
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
`y=sqrt(1+x^2)` `y'=(xy)/(1+x^2)`
Find the order and the degree of the differential equation `x^2 (d^2y)/(dx^2) = { 1 + (dy/dx)^2}^4`
Determine the order and degree of the following differential equations.
`(d^4y)/dx^4 + [1+(dy/dx)^2]^3 = 0`
Fill in the blank:
The order of highest derivative occurring in the differential equation is called ___________ of the differential equation.
Fill in the blank:
Order and degree of a differential equation are always __________ integers.
State whether the following is True or False:
The order of highest derivative occurring in the differential equation is called degree of the differential equation.
Select and write the correct alternative from the given option for the question
The order and degree of `(1 + (("d"y)/("d"x))^3)^(2/3) = 8 ("d"^3y)/("d"x^3)` are respectively
Order of highest derivative occurring in the differential equation is called the ______ of the differential equation
Degree of the given differential equation
`(("d"^3"y")/"dx"^2)^2 = (1 + "dy"/"dx")^(1/3)` is
The differential equation `x((d^2y)/dx^2)^3 + ((d^3y)/dx^3)^2y = x^2` is of ______
The order of the differential equation of all circles which lie in the first quadrant and touch both the axes is ______.
The degree of the differential equation `1/2 ("d"^3"y")/"dx"^3 = {1 + (("d"^2"y")/"dx"^2)}^(5/3)` is ______.
The differential equation of the family of curves y = ex (A cos x + B sin x). Where A and B are arbitary constants is ______.
The order of the differential equation whose general solution is given by `y=C_(1)e^(2x+C_2)+C_3e^x+C_4sin(x+C_5)` is ______.
The order and degree of the differential equation `("d"^2y)/("d"x^2) + (("d"y)/("d"x))^(1/4) + x^(1/5)` = 0, respectively, are ______.
The degree of the differential equation `sqrt(1 + (("d"y)/("d"x))^2)` = x is ______.
Write the sum of the order and the degree of the following differential equation:
`d/(dx) (dy/dx)` = 5
The degree of differential equation `((d^2y)/(dx^2))^3 + ((dy)/(dx))^2 + sin((dy)/(dx)) + 1` = 0 is:
Write the degree of the differential equation (y''')2 + 3(y") + 3xy' + 5y = 0
The degree of the differential equation `dy/dx - x = (y - x dy/dx)^-4` is ______.
The differential equation representing the family of curves y2 = `2c(x + sqrt(c))`, where c is a positive parameter, is of ______.
The order of the differential equation of all parabolas, whose latus rectum is 4a and axis parallel to the x-axis, is ______.
The order and degree of the differential eqµation whose general solution is given by `(d^2y)/(dx^2) + (dy/dx)^50` = In `((d^2y)/dx^2)` respectively, are ______.
Degree of the differential equation `sinx + cos(dy/dx)` = y2 is ______.
The sum of the order and the degree of the differential equation `d/dx[(dy/dx)^3]` is ______.
