Advertisements
Advertisements
प्रश्न
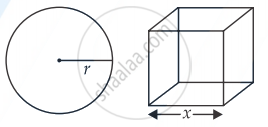
यदि किसी घन तथा गोले के पृष्ठीय क्षेत्रफल का योगफल अचर है तो घन के एक कोर (edge) तथा गोले के व्यास का अनुपात उस समय क्या है जब उनके आयतन का योगफल निम्नतम है?
उत्तर
मान लीजिए x घन का किनारा है और r गोले की त्रिज्या है।
घन का पृष्ठीय क्षेत्रफल = 6x2
तथा गोले का पृष्ठीय क्षेत्रफल = 4πr2
∴ 6x2 + 4πr2 = K ......(स्थिर)
⇒ r = `sqrt(("K" - 6x^2)/(4pi)` .....(i)
घन का आयतन = x3 और गोले का आयतन = `3/4 pi"r"^3`
∴ उनके आयतन का योग (V) = घन का आयतन + गोले का आयतन
⇒ V = `x^3 + 4/3 pi"r"^3`
⇒ V = `x^3 + 4/3 pi xx (("K" - 6x^2)/(4pi))^(3/2)`
दोनों पक्षों में अंतर करना w.r.t. x, हमें मिलता है
`"dV"/"dx" = 3x^2 + (4pi)/3 xx 3/2("K" - 6x^2)^(1/2) (- 12x) xx 1/((4pi)^(3/2)`
= `3x^2 + (2pi)/((4pi)^(3/2)) xx (-12x) ("K" - 6x^2)^(1/2)`
= `3x^2 + 1/(4pi^(1/2)) xx (-12x) ("K" - 6x^2)^(1/2)`
∴ `"dV"/"dx" = 3x^2 - (3x)/sqrt(pi) ("K" - 6x^2)^(1/2)` ....(ii)
स्थानीय उच्चिष्ठ और स्थानीय निम्निष्ठ के लिए, `"dV"/"dx"` = 0
∴ `3x^2 - (3x)/sqrt(pi) ("K" - 6x^2)^(1/2)` = 0
⇒ `3x[x - ("k" - 6x^2)^(1/2)/sqrt(pi)]` = 0
x ≠ 0
∴ `x - ("K" - 6x^2)^(1/2)/sqrt(pi)` = 0
⇒ x = `("K" - 6x^2)^(1/2)/sqrt(pi)`
दोनों पक्षों का वर्ग करने पर, हम प्राप्त करते हैं
x2 = `("K" - 6x^2)/pi`
⇒ `pix^2 = "K" - 6x^2`
⇒ `pix^2 + 6x^2` = K
⇒ `x^2(pi + 6)` = K
⇒ x2 = `"K"/(pi + 6)`
∴ x = `sqrt("K"/(pi + 6)`
अब K के मान को समीकरण (i) में रखने पर, हमें प्राप्त होता है
`6x^2 + 4pir^2 = x^2(pi + 6)`
⇒ `6x^2 + 4pi"r"^2 = pix^2 + 6x^2`
⇒ `4pi"r"^2 = pi"r"^2`
⇒ 4r2 = x2
∴ 2r = x
∴ x:2r = 1:1
अब अवकल समीकरण (ii) w.r.t x, हमारे पास है
`("d"^2"V")/("dx"^2) = 6x - 3/sqrt(pi) "d"/"dx" [x("K" - 6x^2)^(1/2)]`
= `6x - 3/sqrt(pi)[x * 1/(2sqrt("K" - 6x^2)) xx (-12x) + ("K" - 6x^2)^(1/2) * 1]`
= `6x - 3/sqrt(pi) [(-6x^2)/sqrt("K" - 6x^2) + sqrt("K" - 6x^2)]`
= `6x - 3/sqrt(pi) [(-6x^2 + "K" - 6x^2)/sqrt("K" - 6x^2)]`
= `6x + 3/sqrt(pi) [(12x^2 - "K")/sqrt("K" - 6x^2)]`
x = `sqrt("K"/(pi + 6)` लगाए।
= `6sqrt("K"/(pi + 6)) + 3/sqrt(pi)[((12"K")/(pi + 6) - "K")/sqrt("K" - (6"K")/(pi + 6))]`
= `6sqrt("K"/(pi + 6)) + 3/sqrt(pi) [(12"K" - pi"K" - 6"K")/sqrt((pi"K" + 6"K" - 6"K")/(pi + 6))]`
= `6sqrt("K"/(pi + 6)) + 3/sqrt(pi) [(6"K" - pi"K")/sqrt((pi"K")/(pi + 6))]`
= `6sqrt("K"/(pi + 6)) + 3/(pisqrt("K"))[(6"K" - pi"K") sqrt(pi + 6)] > 0`
तो यह निम्निष्ठ है।
इसलिए, आवश्यक अनुपात 1 : 1 है जब संयुक्त मात्रा न्यूनतम है।
APPEARS IN
संबंधित प्रश्न
अवकलज का प्रयोग करके निम्नलिखित में से सन्निकट मान ज्ञात कीजिए।
`(17/81)^(1/4)`
सिद्ध कीजिए कि f (x) = `(log x)/x` द्वारा प्रदत्त फलन x = e पर उच्चतम है।
वक्रों `x^2/"a"^2 - y^2/"b"^2` = 1 तथा xy = c2 के लम्बकोणीय प्रतिच्छेदन के लिए प्रतिबंध ज्ञात कीजिए।
फलन f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105` के सभी स्थानीय उच्चिष्ठ तथा स्थानीय निम्निष्ठ बिंदुओं को ज्ञात कीजिए।
वक्र y2 = 4ax तथा x2 = 4by का प्रतिच्छेद कोण ज्ञात कीजिए।
सिद्ध कीजिए कि वक्र x = 3cos θ – cos3θ, y = 3sinθ – sin3θ के किसी बिंदु पर अभिंलब का समीकरण 4 (y cos3θ – x sin3θ) = 3 sin 4θ
वक्र y2 = x पर वह बिंदु जहाँ स्पर्श रेखा x-अक्ष से `pi/4` कोण बनाती है।
यदि f (x) = `1/(4x^2 + 2x + 1)`, तो इसका उच्चतम मान ______ है।
यदि f (x) = sinx तो अंतराल `[(-pi)/2, pi/2]` में f का निम्निष्ठ मान ______ है।
sinx + cosx का उच्चिष्ठ मान ______ है।
यदि किसी वृत्त का क्षेत्रफल एक समान दर से बढ़ता है, तो सिद्ध कीजिए कि उसका परिमाप (परिधि) उसकी त्रिज्या के व्युत्क्रमानुपाती होता है
कोण θ, 0 < θ < `π/2`, ज्ञात कीजिए जो अपने sine से दोगुनी तेजी से बढ़ता है।
किसी तरनताल को सफाई के लिए खाली करना है।यदि ताल को बंद करने के t seconds बाद ताल में पानी की मात्रा, लिटर में, L से निरूपित होती है तथा L = 200 (10 – t)2 तो 5 seconds में अंत में पानी कितनी तेजी से बाहर निकल रहा है? प्रथम 5 seconds में पानी के बाहर निकलने की औसत दर क्या है?
किसी घन का आयतन एक अचर दर से बढ़ रहा है। सिद्ध कीजिए कि उसके पृष्ठीय क्षेत्रफल की वृद्धि उसकी भुजा की व्युत्क्रमानुपाती है।
वक्र y = 4 – x2 तथा y = x2 का प्रतिच्छेद-कोण ज्ञात कीजिए।
सिद्ध कीजिए कि a ≥ 1 के लिए f (x) = `sqrt3` sinx - cosx - 2ax + b, R में हासमान फलन है।
किस बिंदु पर, वक्र y = – x3 + 3x2 + 9x – 27 की प्रवणता उच्चतम है? उच्चतम प्रवणता भी ज्ञात कीजिए।
किसी नगर में एक टेलीफोन कंपनी की सूची में 500 ग्राहक हैं और वह प्रत्येक ग्राहक से प्रतिवर्ष 300 रु निश्चित शुल्क वसूलती हैं। कंपनी वार्षिक शुल्क बढ़ाना चाहती है, और ऐसा माना जाता है कि प्रत्येक 1 रु की वृद्धि करने पर एक ग्राहक टेलीफोन सेवा लेना समाप्त कर देगा।ज्ञात कीजिए कि कितनी वृद्धि करने से महत्तम (उच्चतम) लाभ होगा।
वर्गाकार आधार तथा ऊर्ध्वाधर पृष्ठ वाले धातु के किसी बाक्स में 1024 cm3 वस्तु आती है। शीर्ष तथा आधार के पृष्ठों के माल (वस्तु) का मूल्य Rs 5/cm2 है तथा पृष्ठों के मान का मूल्य Rs 2.50/cm2 हैं। बाक्स का निम्नतम मूल्य ज्ञात कीजिए।
किसी समबाहु त्रिभुज की भुजाएँ 2 cm/sec की दर से बढ़ रही हैं। जब भुजा 10 cm है, त्रिभुज का क्षेत्रफल ______ की दर से बढ़ता है।
बिंदु (0, 0) पर वक्र y = `x^(1/5)` की ______
यदि वक्र ay + x2 = 7 तथा x3 = y बिंदु (1, 1) पर लंबवत काटते हैं, तो a का मान है ______
दो वक्र x3 – 3xy2 + 2 = 0 तथा 3x2 y – y3 – 2 = 0 किस कोण पर प्रतिच्छेद करते हैं:
मान लीजिए कि f : R → R, f (x) = 2x + cosx द्वारा परिभाषित है, तो f ______
sin x . cos x का उच्चतम मान है ______
f (x) = 2 sin3x + 3 cos3x का मान x = `(5pi)/6`, पर ______
वक् y = –x3 + 3x2 + 9x – 27 की उच्चतम प्रवणता ______
f(x) = xx का स्तब्ध बिंदु है ______
