Advertisements
Advertisements
प्रश्न
वर्गाकार आधार तथा ऊर्ध्वाधर पृष्ठ वाले धातु के किसी बाक्स में 1024 cm3 वस्तु आती है। शीर्ष तथा आधार के पृष्ठों के माल (वस्तु) का मूल्य Rs 5/cm2 है तथा पृष्ठों के मान का मूल्य Rs 2.50/cm2 हैं। बाक्स का निम्नतम मूल्य ज्ञात कीजिए।
उत्तर
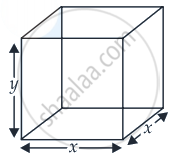
मान लीजिए x वर्गाकार आधार की भुजा है और y ऊर्ध्वाधर भुजाओं की लंबाई है।
आधार और तल का क्षेत्रफल = 2x2 cm2
∴ आवश्यक सामग्री की लागत = ₹ 5 × 2x2
= ₹ 10x2
4 भुजाओं का क्षेत्रफल = 4xy cm2
∴ चारों पक्षों के लिए सामग्री की लागत
= ₹ 2.50 x 4xy
= ₹ 10xy
कुल लागत C = 10x2 + 10xy .....(i)
बाक्स का नया आयतन = x × x × y
⇒ 1024 = x2y
∴ y = `1024/x^2` ....(ii)
y का मान समीकरण (i) में रखने पर हमें प्राप्त होता है
C = `10x^2 + 10x xx 1024/x^2`
⇒ C = `10x^2 + 10240/x`
दोनों पक्षों में अंतर करना w.r.t. x, हमें मिलता है
`"dC"/"dx" = 20x - 10240/x^2` ....(iii)
`"dC"/"dx"` = 0 स्थानीय उच्चिष्ठ और स्थानीय निम्निष्ठ के लिए,
`20 - 102400/x^2` = 0
⇒ 20x3 – 10240 = 0
⇒ x3 = 512
⇒ x = 8 cm
अब समीकरण (ii) से
y = `10240/(8)^2`
= `10240/64`
= 16 cm
∴ प्रयुक्त सामग्री की लागत C = 10x2 + 10xy
= 10 × 8 × 8 + 10 × 8 × 16
= 640 + 1280
= 1920
अब अवकलन समीकरण (iii) से हम प्राप्त करते हैं
`("d"^2"C")/("dx"^2) = 20 + 20480/x^3`
x = 8 रखो
= `20 + 20480/(8)^3`
= `20 + 20480/512`
= 20 + 40 = 60 > 0 निम्निष्ठ
अत: अभीष्ट लागत ₹ 1920 है जो कि न्यूनतम है।
APPEARS IN
संबंधित प्रश्न
वक्र y = 5x – 2x3 के लिए, यदि x में 2 इकाई/से. की दर से वृद्धि हो रही है, तो x = 3 पर वक्र का प्रावण्य कितनी तीव्रता से परिवर्तित हो रहा है?
निर्धारित कीजिए कि x के किन मानों के लिए, फलन y = `x^4 – (4x^3)/3` वर्धमान है तथा किन मानों के लिए, यह हासमान है।
अवकलों के प्रयोग द्वारा `sqrt(0.082)` का सन्निकट मान ज्ञात कीजिए।
सिद्ध कीजिए कि `x + 1/x` का स्थानीय उच्चतम मीन उसके स्थानीय निम्नतम मान से कम है।
किसी शांकवीय बर्तन के शीर्ष के एक छोटे छिद्र से, जिसका अक्ष ऊर्घ्वाधर है, पानी 1 cu cm/sec की दर से बह रहा है। बर्तन में पानी के सतह की तिर्यक ऊँचाई के घटने की दर उस समय ज्ञात कीजिए जब तिर्यक ऊँचाई 4 cm हैं। शांकवीय बर्तन का शीर्ष कोण `pi/6` है।
f(x) = secx + log cos2x, 0 < x < 2π का उच्चतम तथा निम्नतम मान ज्ञात कीजिए।
उस महत्तम आयत का क्षेत्रफल ज्ञात कीजिए, जो दीर्घवृत्त `x^2/a^2 + y^2/b^2` = 1 के अंतर्गत स्थित है।
अंतराल `[-pi/2, pi/2]` में फलन f (x) = sin2x – x, के उच्चतम तथा निम्नितम मानों का अंतर ज्ञात कीजिए।
वक्र y2 = x पर वह बिंदु जहाँ स्पर्श रेखा x-अक्ष से `pi/4` कोण बनाती है।
a के वे मान जिनके लिए y = x2 + ax + 25 x-अक्ष को स्पर्श करता है, ______ है।
मान लीजिए कि c पर f का द्वितीय अवकलज है, इस प्रकार कि f ′(c) = 0 तथा f ″(c) > 0, तो c पर फलन ______ है।
किसी गोले के आयतन के परिवर्तन की दर उसके पृष्ठीय क्षेत्रफल के सापेक्ष, जब उसकी त्रिज्या 2cm है, ______ है।
नमक का एक गोलाकार गेंद पानी में इस प्रकार घुल रहा है कि किसी क्षण उसके आयतन के घटने की दर उसके पृष्ठीय क्षेत्रफल के समानुपाती है। सिद्ध कीजिए कि उसकी त्रिज्या एक अचर दर से घट रही है।
यदि किसी वृत्त का क्षेत्रफल एक समान दर से बढ़ता है, तो सिद्ध कीजिए कि उसका परिमाप (परिधि) उसकी त्रिज्या के व्युत्क्रमानुपाती होता है
(1.999)5 का सन्निकट मान ज्ञात कीजिए।
एक खोखले बेलनाकार खोल, जिसकी आंतरिक तथा बाह्य त्रिज्याएँ क्रमश: 3 cm तथा 3.0005 cm हैं, में धातु के आयतन का सन्निकट मान ज्ञात कीजिए।
किसी तरनताल को सफाई के लिए खाली करना है।यदि ताल को बंद करने के t seconds बाद ताल में पानी की मात्रा, लिटर में, L से निरूपित होती है तथा L = 200 (10 – t)2 तो 5 seconds में अंत में पानी कितनी तेजी से बाहर निकल रहा है? प्रथम 5 seconds में पानी के बाहर निकलने की औसत दर क्या है?
सिद्ध कीजिए कि वक्र xy = 4 तथा x2 + y2 = 8, एक दूसरे को स्पर्श करते हैं।
36 cm परिमाप वाले आयत की विमाएँ ज्ञात कीजिए जिसे उसकी भुजाओं में से किसी एक के चारों ओर घुमाने पर अधिक से अधिक सम्भव आयतन प्रसर्प (sweep) हो।
यदि किसी घन तथा गोले के पृष्ठीय क्षेत्रफल का योगफल अचर है तो घन के एक कोर (edge) तथा गोले के व्यास का अनुपात उस समय क्या है जब उनके आयतन का योगफल निम्नतम है?
किसी समबाहु त्रिभुज की भुजाएँ 2 cm/sec की दर से बढ़ रही हैं। जब भुजा 10 cm है, त्रिभुज का क्षेत्रफल ______ की दर से बढ़ता है।
यदि y = x4 – 10 तथा यदि x, 2 से 1.99 तक परिवर्तित होता है, तो y का परिवर्तन क्या (कितना) है,
दो वक्र x3 – 3xy2 + 2 = 0 तथा 3x2 y – y3 – 2 = 0 किस कोण पर प्रतिच्छेद करते हैं:
y = x(x – 3)2, x के नीचे दिए हुए मानों के लिए हासमान है,
बहुपद x3 – 18x2 + 96x का, अंतराल [0, 9] में, निम्नतम मान ______
फलन f (x) = 2x3 – 3x2 – 12x + 4 के ______
f (x) = 2 sin3x + 3 cos3x का मान x = `(5pi)/6`, पर ______
f(x) = xx का स्तब्ध बिंदु है ______
वक् y = 4x2 + 2x – 8 तथा, y = x3 – x + 13 एक दूसरे को बिंदु ______ पर स्पर्श करते हैं।
