HSC Science (General)
HSC Arts (English Medium)
HSC Science (Electronics)
HSC Science (Computer Science)
Academic Year: 2016-2017
Date: जुलै 2017
Advertisements
The inverse of the matrix `[[1,-1],[2,3]]` is ...............
(A) `1/5[[3,-1],[-2,1]]`
(B) `1/5[[3,1],[-2,1]]`
(C) `1/5[[-3,1],[-2,1]]`
(D) `1/5[[3,-1],[2,-1]]`
Chapter: [0.02] Matrices
If `bara=3hati-hatj+4hatk, barb=2hati+3hatj-hatk, barc=-5hati+2hatj+3hatk` then `bara.(barbxxbarc)=`
(A) 100
(B) 101
(C) 110
(D) 109
Chapter: [0.015] Vectors [0.07] Vectors
If a line makes angles 90°, 135°, 45° with the X, Y, and Z axes respectively, then its direction cosines are _______.
(A) `0,1/sqrt2,-1/sqrt2`
(B) `0,-1/sqrt2,-1/sqrt2`
(C) `1,1/sqrt2,1/sqrt2`
(D) `0,-1/sqrt2,1/sqrt2`
Chapter: [0.08] Three Dimensional Geometry
`barr=(hati-2hatj+3hatk)+lambda(2hati+hatj+2hatk)` is parallel to the plane `barr.(3hati-2hatj+phatk)=10`, find the value of p.
Chapter: [0.1] Plane
If a line makes angles α, β, γ with co-ordinate axes, prove that cos 2α + cos2β + cos2γ+ 1 = 0.
Chapter: [0.03] Trigonometric Functions
Write the negations of the following statements:
a.`forall n in N, n+7>6`
b. The kitchen is neat and tidy.
Chapter: [0.01] Mathematical Logic
Find the angle between the lines whose direction ratios are 4, –3, 5 and 3, 4, 5.
Chapter: [0.08] Three Dimensional Geometry
If `bara, barb, barc` are position vectors of the points A, B, C respectively such that `3bara+ 5barb-8barc = 0`, find the ratio in which A divides BC.
Chapter: [0.07] Vectors
If `tan^-1(2x)+tan^-1(3x)=pi/4`, then find the value of ‘x’.
Chapter: [0.03] Trigonometric Functions
Write the converse, inverse and contrapositive of the following statement.
“If it rains then the match will be cancelled.”
Chapter: [0.01] Mathematical Logic
Find p and q if the equation px2 – 8xy + 3y2 + 14x + 2y + q = 0 represents a pair of prependicular lines.
Chapter: [0.013999999999999999] Pair of Straight Lines
Find the equation of the plane passing through the intersection of the planes 3x + 2y – z + 1 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Chapter: [0.1] Plane
Let `A(bara)` and `B(barb)` be any two points in the space and `R(barr)` be a point on the line segment AB dividing it internally in the ratio m : n, then prove that `bar r=(mbarb+nbara)/(m+n)` . Hence find the position vector of R which divides the line segment joining the points A(1, –2, 1) and B(1, 4, –2) internally in the ratio 2 : 1.
Chapter: [0.013999999999999999] Pair of Straight Lines [0.09] Line
Advertisements
The angles of the ΔABC are in A.P. and b:c=`sqrt3:sqrt2` then find`angleA,angleB,angleC`
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
Find the cartesian equation of the line passing throught the points A(3, 4, -7) and B(6,-1, 1).
Chapter: [0.04] Pair of Straight Lines
Find the vector equation of a line passing through the points A(3, 4, –7) and B(6, –1, 1).
Chapter: [0.1] Plane
Find the general solution of the equation sin 2x + sin 4x + sin 6x = 0
Chapter: [0.03] Trigonometric Functions
Find the symbolic form of the following switching circuit, construct its switching table and interpret it.
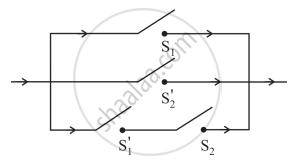
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
If `A=[[1,-1,2],[3,0,-2],[1,0,3]]` verify that A (adj A) = |A| I.
Chapter: [0.02] Matrices
A company manufactures bicycles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours available and machine B has maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are Rs. 180 for a bicycle and Rs. 220 for a tricycle, formulate and solve the L.P.P. to determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Chapter: [0.017] Linear Programming [0.11] Linear Programming Problems
If θ is the measure of acute angle between the pair of lines given by `ax^2+2hxy+by^2=0,` then prove that `tantheta=|(2sqrt(h^2-ab))/(a+b)|,a+bne0`
Chapter: [0.04] Pair of Straight Lines
find the acute angle between the lines
x2 – 4xy + y2 = 0.
Chapter: [0.04] Pair of Straight Lines
Given f (x) = 2x, x < 0
= 0, x ≥ 0
then f (x) is _______ .
discontinuous and not differentiable at x = 0
continuous and differentiable at x = 0
discontinuous and differentiable at x = 0
continuous and not differentiable at x = 0
Chapter: [0.12] Continuity
If `int_0^alpha(3x^2+2x+1)dx=14` then `alpha=`
(A) 1
(B) 2
(C) –1
(D) –2
Chapter: [0.15] Integration
The function f (x) = x3 – 3x2 + 3x – 100, x∈ R is _______.
(A) increasing
(B) decreasing
(C) increasing and decreasing
(D) neither increasing nor decreasing
Chapter: [0.022000000000000002] Applications of Derivatives [0.14] Applications of Derivative
Differentiate 3x w.r.t. log3x
Chapter: [0.12] Continuity [0.13] Differentiation
Check whether the conditions of Rolle’s theorem are satisfied by the function
f (x) = (x - 1) (x - 2) (x - 3), x ∈ [1, 3]
Chapter: [0.14] Applications of Derivative
Evaluate: `int sqrt(tanx)/(sinxcosx) dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Advertisements
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Chapter: [0.16] Applications of Definite Integral
Given X ~ B (n, p)
If n = 10 and p = 0.4, find E(X) and var (X).
Chapter: [0.027999999999999997] Binomial Distribution [0.2] Bernoulli Trials and Binomial Distribution
If the function `f(x)=(5^sinx-1)^2/(xlog(1+2x))` for x ≠ 0 is continuous at x = 0, find f (0).
Chapter: [0.12] Continuity
The probability mass function for X = number of major defects in a randomly selected
appliance of a certain type is
| X = x | 0 | 1 | 2 | 3 | 4 |
| P(X = x) | 0.08 | 0.15 | 0.45 | 0.27 | 0.05 |
Find the expected value and variance of X.
Chapter: [0.027999999999999997] Binomial Distribution [0.2] Bernoulli Trials and Binomial Distribution
Suppose that 80% of all families own a television set. If 5 families are interviewed at random, find the probability that
a. three families own a television set.
b. at least two families own a television set.
Chapter: [0.19] Probability Distribution
Find the approximate value of cos (60° 30').
(Given: 1° = 0.0175c, sin 60° = 0.8660)
Chapter: [0.022000000000000002] Applications of Derivatives [0.14] Applications of Derivative
The rate of growth of bacteria is proportional to the number present. If, initially, there were
1000 bacteria and the number doubles in one hour, find the number of bacteria after 2½
hours.
[Take `sqrt2` = 1.414]
Chapter: [0.14] Applications of Derivative
Prove that:
`{:(int_(-a)^a f(x) dx = 2 int_0^a f(x) dx",", "If" f(x) "is an even function"),( = 0",", "if" f(x) "is an odd function"):}`
Chapter: [0.024] Definite Integration
If f (x) is continuous on [–4, 2] defined as
f (x) = 6b – 3ax, for -4 ≤ x < –2
= 4x + 1, for –2 ≤ x ≤ 2
Show that a + b =`-7/6`
Chapter: [0.12] Continuity
If u and v are two functions of x then prove that
`intuvdx=uintvdx-int[du/dxintvdx]dx`
Hence evaluate, `int xe^xdx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Probability distribution of X is given by
| X = x | 1 | 2 | 3 | 4 |
| P(X = x) | 0.1 | 0.3 | 0.4 | 0.2 |
Find P(X ≥ 2) and obtain cumulative distribution function of X
Chapter: [0.027000000000000003] Probability Distributions [0.19] Probability Distribution
Solve the differential equation `dy/dx -y =e^x`
Chapter: [0.17] Differential Equation
If y = f (x) is a differentiable function of x such that inverse function x = f –1(y) exists, then
prove that x is a differentiable function of y and
`dx/dy=1/(dy/dx)`, Where `dy/dxne0`
Hence if `y=sin^-1x, -1<=x<=1 , -pi/2<=y<=pi/2`
then show that `dy/dx=1/sqrt(1-x^2)`, where `|x|<1`
Chapter: [0.13] Differentiation
Evaluate: `∫8/((x+2)(x^2+4))dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 12th Standard Board Exam Mathematics and Statistics with solutions 2016 - 2017
Previous year Question paper for Maharashtra State Board 12th Standard Board Exam Maths and Stats-2017 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics and Statistics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 12th Standard Board Exam.
How Maharashtra State Board 12th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Mathematics and Statistics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
