Advertisements
Online Mock Tests
Chapters
2: Matrics
3: Trigonometric Functions
4: Pair of Straight Lines
5: Vectors
6: Line and Plane
7: Linear Programming
![Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board chapter 1 - Mathematical Logic Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board chapter 1 - Mathematical Logic - Shaalaa.com](/images/mathematics-and-statistics-1-arts-and-science-english-12-standard-hsc-maharashtra-state-board_6:a050ad90c0124a57a3b775cc0f8ff57b.JPG)
Advertisements
Solutions for Chapter 1: Mathematical Logic
Below listed, you can find solutions for Chapter 1 of Maharashtra State Board Balbharati for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board.
Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board 1 Mathematical Logic Exercise 1.1 [Pages 6 - 7]
State which of the following is the statement. Justify. In case of a statement, state its truth value.
5 + 4 = 13
State which of the following is the statement. Justify. In case of a statement, state its truth value.
x – 3 = 14
State which of the following is the statement. Justify. In case of a statement, state its truth value.
Close the door.
State which of the following is the statement. Justify. In case of a statement, state its truth value.
Zero is a complex number.
State which of the following is the statement. Justify. In case of a statement, state its truth value.
Please get me breakfast.
State which of the following is the statement. Justify. In case of a statement, state its truth value.
Congruent triangles are similar.
State which of the following is the statement. Justify. In case of a statement, state its truth value.
x2 = x
State which of the following is the statement. Justify. In case of a statement, state its truth value.
A quadratic equation cannot have more than two roots.
State which of the following is the statement. Justify. In case of a statement, state its truth value.
Do you like Mathematics?
State which of the following is the statement. Justify. In case of a statement, state its truth value.
The sunsets in the west
State which of the following is the statement. Justify. In case of a statement, state its truth value.
All real numbers are whole numbers.
State which of the following is the statement. Justify. In case of a statement, state its truth value.
Can you speak in Marathi?
State which of the following is the statement. Justify. In case of a statement, state its truth value.
x2 – 6x – 7 = 0, when x = 7
State which of the following is the statement. Justify. In case of a statement, state its truth value.
The sum of cube roots of unity is zero.
State which of the following is the statement. Justify. In case of a statement, state its truth value.
It rains heavily.
Write the following compound statement symbolically.
Nagpur is in Maharashtra and Chennai is in Tamil Nadu.
Write the following compound statements symbolically.
Triangle is equilateral or isosceles
Write the following compound statement symbolically.
The angle is right angle if and only if it is of measure 90°.
Write the following compound statement symbolically.
Angle is neither acute nor obtuse.
Write the following compound statement symbolically.
If Δ ABC is right-angled at B, then m∠A + m∠C = 90°
Write the following compound statement symbolically.
Hima Das wins gold medal if and only if she runs fast.
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Write the truth values of the following.
4 is odd or 1 is prime.
Write the truth values of the following.
64 is a perfect square and 46 is a prime number.
Write the truth values of the following.
5 is a prime number and 7 divides 94.
Write the truth values of the following.
It is not true that 5−3i is a real number.
Write the truth value of the following.
If 3 × 5 = 8 then 3 + 5 = 15.
Write the truth value of the following.
Milk is white if and only if sky is blue.
Write the truth values of the following.
24 is a composite number or 17 is a prime number.
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
p ∨ (q ∧ r)
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
(p → q) ∨ (r → s)
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
(q ∧ r) ∨ (∼ p ∧ s)
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
(p → q) ∧ ∼ r
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
(∼ r ↔ p) → ∼ q
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
[∼ p ∧ (∼ q ∧ r)] ∨ [(q ∧ r) ∨ (p ∧ r)]
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
[(∼ p ∧ q) ∧ ∼ r] ∨ [(q → p) → (∼ s ∨ r)]
If the statement p, q are true statement and r, s are false statement then determine the truth value of the following:
∼ [(∼ p ∧ r) ∨ (s → ∼ q)] ↔ (p ∧ r)
Write the negation of the following.
Tirupati is in Andhra Pradesh.
Write the negation of the following.
3 is not a root of the equation x2 + 3x – 18 = 0
Write the negation of the following.
`sqrt2` is a rational number.
Write the negation of the following.
Polygon ABCDE is a pentagon.
Write the negation of the following.
Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board 1 Mathematical Logic Exercise 1.2 [Page 13]
Construct the truth table of the following statement pattern.
[(p → q) ∧ q] → p
Construct the truth table of the following statement pattern.
(p ∧ ∼q) ↔ (p → q)
Construct the truth table of the following statement pattern.
(p ∧ q) ↔ (q ∨ r)
Construct the truth table of the following statement pattern.
p → [∼ (q ∧ r)]
Construct the truth table of the following statement pattern.
∼ p ∧ [(p ∨ ∼ q) ∧ q]
Construct the truth table of the following statement pattern.
(∼ p → ∼ q) ∧ (∼ q → ∼ p)
Construct the truth table of the following statement pattern.
(q → p) ∨ (∼ p ↔ q)
Construct the truth table of the following statement pattern.
[p → (q → r)] ↔ [(p ∧ q) → r]
Construct the truth table of the following statement pattern.
p → [∼ (q ∧ r)]
Construct the truth table of the following statement pattern.
(p ∨ ∼ q) → (r ∧ p)
Using truth table, prove that ~ p ∧ q ≡ (p ∨ q) ∧ ~ p
Using the truth table prove the following logical equivalence.
∼ (p ∨ q) ∨ (∼ p ∧ q) ≡ ∼ p
Using the truth table prove the following logical equivalence.
p ↔ q ≡ ∼ [(p ∨ q) ∧ ∼ (p ∧ q)]
Using the truth table prove the following logical equivalence.
p → (q → p) ≡ ∼ p → (p → q)
Using the truth table prove the following logical equivalence.
(p ∨ q) → r ≡ (p → r) ∧ (q → r)
Using the truth table prove the following logical equivalence.
p → (q ∧ r) ≡ (p → q) ∧ (p → r)
Using the truth table prove the following logical equivalence.
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Using the truth table prove the following logical equivalence.
[∼ (p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
Using the truth table proves the following logical equivalence.
∼ (p ↔ q) ≡ (p ∧ ∼ q) ∨ (q ∧ ∼ p)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
(p ∧ q) → (q ∨ p)
Tautology
Contradiction
Contingency
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
(p → q) ↔ (∼ p ∨ q)
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Examine whether the following logical statement pattern is a tautology, contradiction, or contingency.
[(p→q) ∧ q]→p
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
[(p → q) ∧ ∼ q] → ∼ p
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
(p ↔ q) ∧ (p → ∼ q)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
∼ (∼ q ∧ p) ∧ q
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
(p ∧ ∼ q) ↔ (p → q)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
(∼ p → q) ∧ (p ∧ r)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
[p → (∼ q ∨ r)] ↔ ∼ [p → (q → r)]
Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board 1 Mathematical Logic Exercise 1.3 [Pages 17 - 18]
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of the following.
∃ x ∈ A such that x – 8 = 1
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of the following.
∀ x ∈ A, x2 + x is an even number
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of the following.
∃ x ∈ A such that x2 < 0
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of the following.
∀ x ∈ A, x is an even number.
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of the following.
∃ x ∈ A such that 3x + 8 > 40
If A = {3, 5, 7, 9, 11, 12}, determine the truth value of the following.
∀ x ∈ A, 2x + 9 > 14
Write the dual of the following.
p ∨ (q ∧ r)
Write the dual of the following.
p ∧ (q ∧ r)
Write the dual of the following.
(p ∨ q) ∧ (r ∨ s)
Write the dual of the following.
p ∧ ∼ q
Write the dual of the following.
(∼ p ∨ q) ∧ (∼ r ∧ s)
Write the dual of the following.
∼ p ∧ (∼ q ∧ (p ∨ q) ∧ ∼ r)
Write the dual of the following.
[∼ (p ∨ q)] ∧ [p ∨ ∼ (q ∧ ∼ s)]
Write the dual of the following.
c ∨ {p ∧ (q ∨ r)}
Write the dual of the following.
∼ p ∨ (q ∧ r) ∧ t
Write the dual of the following.
(p ∨ q) ∨ c
Write the negation of the following.
x + 8 > 11 or y – 3 = 6
Write the negation of the following.
11 < 15 and 25 > 20
Write the negation of the following.
Quadrilateral is a square if and only if it is a rhombus.
Write the negation of the following.
It is cold and raining.
Write the negation of the following.
If it is raining then we will go and play football.
Write the negation of the following.
`sqrt2` is a rational number.
Write the negation of the following.
All-natural numbers are whole numbers.
Write the negation of the following.
∀ n ∈ N, n2 + n + 2 is divisible by 4.
Write the negation of the following.
∃ x ∈ N such that x – 17 < 20
Write converse, inverse and contrapositive of the following statement.
If x < y then x2 < y2 (x, y ∈ R)
Write converse, inverse and contrapositive of the following statement.
A family becomes literate if the woman in it is literate.
Write converse, inverse and contrapositive of the following statement.
If surface area decreases then pressure increases.
Write converse, inverse and contrapositive of the following statement. "If voltage increases then current decreases".
Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board 1 Mathematical Logic Exercise 1.4 [Page 21]
Using the rule of negation write the negation of the following with justification.
∼ q → p
Using the rule of negation write the negation of the following with justification.
p ∧ ∼ q
Using the rule of negation write the negation of the following with justification.
p ∨ ∼ q
Using the rule of negation write the negation of the following with justification.
(p ∨ ∼ q) ∧ r
Using the rule of negation write the negation of the following with justification.
p → (p ∨ ∼ q)
Using the rule of negation write the negation of the following with justification.
∼ (p ∧ q) ∨ (p ∨ ∼ q)
Using the rule of negation write the negation of the following with justification.
(p ∨ ∼ q) → (p ∧ ∼ q)
Using the rule of negation write the negation of the following with justification.
(∼ p ∨ ∼ q) ∨ (p ∧ ∼ q)
Rewrite the following statement without using if ...... then.
If a man is a judge then he is honest.
Rewrite the following statement without using if ...... then.
It 2 is a rational number then `sqrt2` is irrational number.
Rewrite the following statement without using if ...... then.
It f(2) = 0 then f(x) is divisible by (x – 2).
Without using the truth table show that P ↔ q ≡ (p ∧ q) ∨ (~ p ∧ ~ q)
Without using truth table prove that:
(p ∨ q) ∧ (p ∨ ∼ q) ≡ p
Without using truth table prove that:
(p ∧ q) ∨ (∼ p ∧ q) ∨ (p ∧ ∼ q) ≡ p ∨ q
Without using truth table prove that:
∼ [(p ∨ ∼ q) → (p ∧ ∼ q)] ≡ (p ∨ ∼ q) ∧ (∼ p ∨ q)
Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board 1 Mathematical Logic Exercise 1.5 [Pages 29 - 30]
Express the following circuit in the symbolic form of logic and writ the input-output table.
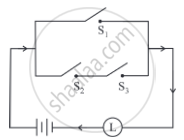
Express the following circuit in the symbolic form of logic and write the input-output table.
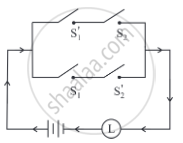
Express the following circuit in the symbolic form of logic and write the input-output table.

Express the following circuit in the symbolic form of logic and write the input-output table.
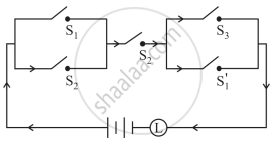
Express the following circuit in the symbolic form of logic and writ the input-output table.

Express the following circuit in the symbolic form of logic and writ the input-output table.
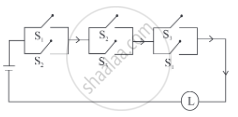
Construct the switching circuit of the following:
(∼ p ∧ q) ∨ (p ∧ ∼ r)
Construct the switching circuit of the following:
(p ∧ q) ∨ [∼ p ∧ (∼ q ∨ p ∨ r)]
Construct the switching circuit of the following:
(p ∧ r) ∨ (∼ q ∧ ∼ r)] ∧ (∼ p ∧ ∼ r)
Construct the switching circuit of the following:
(p ∧ ∼ q ∧ r) ∨ [p ∧ (∼ q ∨ ∼ r)]
Construct the switching circuit of the following:
p ∨ (∼ p) ∨ (∼ q) ∨ (p ∧ q)
Construct the switching circuit of the following:
(p ∧ q) ∨ (∼ p) ∨ (p ∧ ∼ q)
Give an alternative equivalent simple circuit for the following circuit:

Give an alternative equivalent simple circuit for the following circuit:
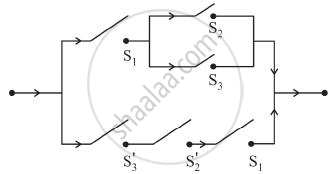
Find the symbolic form of the following switching circuit, construct its switching table and interpret it.
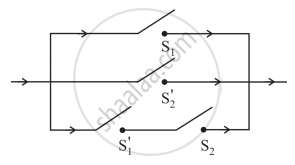
Write the symbolic form of the following switching circuit construct its switching table and interpret it.
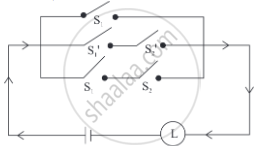
Write the symbolic form of the following switching circuit construct its switching table and interpret it.

Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
p ∨ (q ∧ ∼ q)
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(∼ p ∧ q) ∨ (∼ p ∧ ∼ q) ∨ (p ∧ ∼ q)
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
[p ∨ ( ∼ q) ∨ (∼ r)] ∧ [p ∨ (q ∧ r)]
Obtain the simple logical expression of the following. Draw the corresponding switching circuit.
(p ∧ q ∧ ∼ p) ∨ (∼ p ∧ q ∧ r) ∨ (p ∧ ∼ q ∧ r) ∨ (p ∧ q ∧ r)
Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board 1 Mathematical Logic Miscellaneous Exercise 1 [Pages 32 - 35]
If p ∧ q is false and p ∨ q is true, then ______ is not true.
p ∨ q
p ↔ q
∼p ∨ ∼q
q ∨ ∼p
(p ∧ q) → r is logically equivalent to ________.
p → (q → r)
(p ∧ q) → ∼r
(∼p ∨ ∼q) → ∼r
(p ∨ q) → r
Inverse of statement pattern (p ∨ q) → (p ∧ q) is ________ .
(p ∧ q) → (p ∨ q)
∼ (p ∨ q) → (p ∧ q)
(∼p ∧ ∼q) → (∼p ∨ ∼q)
(∼p ∨ ∼q) → (∼p ∧ ∼q)
If p ∧ q is F, p → q is F then the truth values of p and q are ________.
T, T
T, F
F, T
F, F
Select and write the correct answer from the given alternative of the following question:
The negation of inverse of ∼p → q is ________.
q ∧ p
∼p ∧ ∼q
p ∧ q
∼q → ∼p
The negation of p ∧ (q → r) is ________.
∼p ∧ (∼q → ∼r)
p ∨ (∼q ∨ r)
∼p ∧ (∼q → ∼r)
∼p ∨ (q ∧ ∼r)
If A = {1, 2, 3, 4, 5} then which of the following is not true?
∃ x ∈ A such that x + 3 = 8
∃ x ∈ A such that x + 2 < 9
∀ x ∈ A, x + 6 ≥ 9
∃ x ∈ A such that x + 6 < 10
Which of the following sentence is the statement in logic? Justify. Write down the truth value of the statement:
4! = 24.
Which of the following sentence is the statement in logic? Justify. Write down the truth value of the statement:
π is an irrational number.
Which of the following sentence is the statement in logic? Justify. Write down the truth value of the statement:
India is a country and Himalayas is a river.
Which of the following sentence is the statement in logic? Justify. Write down the truth value of the statement:
Please get me a glass of water.
Which of the following sentence is the statement in logic? Justify. Write down the truth value of the statement:
cos2θ − sin2θ = cos2θ for all θ∈R.
Which of the following sentence is the statement in logic? Justify. Write down the truth value of the statement:
If x is a whole number then x + 6 = 0.
`sqrt5` is an irrational but `3sqrt5` is a complex number.
Write the truth value of the following statement:
∀ n ∈ N, n2 + n is even number while n2 – n is an odd number.
Write the truth value of the following statement:
∃ n ∈ N such that n + 5 > 10.
Write the truth value of the following statement:
The square of any even number is odd or the cube of any odd number is odd.
Write the truth value of the following statement:
In ΔABC if all sides are equal then its all angles are equal.
Write the truth value of the following statement:
∀ n ∈ N, n + 6 > 8.
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, determine the truth value of the following statement:
∃ x ∈ A such that x + 8 = 15
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, determine the truth value of the following statement:
∀ x ∈ A, x + 5 < 12.
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, determine the truth value of the following statement:
∃ x ∈ A, such that x + 7 ≥ 11.
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, determine the truth value of the following statement:
∀ x ∈ A, 3x ≤ 25.
Write the negation of the following:
∀ n ∈ A, n + 7 > 6.
Write the negation of the following:
∃ x ∈ A, such that x + 9 ≤ 15.
Write the negation of the following:
Some triangles are equilateral triangle.
Construct the truth table of the following:
p → (q → p)
Construct the truth table of the following:
(∼p ∨ ∼q) ↔ [∼(p ∧ q)]
Construct the truth table of the following:
∼ (∼p ∧ ∼q) ∨ q
Construct the truth table of the following:
[(p ∧ q) ∨ r] ∧ [∼r ∨ (p ∧ q)]
Construct the truth table of the following:
[(∼p ∨ q) ∧ (q → r)] → (p → r)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
[(p → q) ∧ ∼ q] → ∼ p
Determine whether the following statement pattern is a tautology, contradiction, or contingency:
[(p ∨ q) ∧ ∼p] ∧ ∼q
Determine whether the following statement pattern is a tautology, contradiction, or contingency:
(p → q) ∧ (p ∧ ∼q)
Determine whether the following statement pattern is a tautology, contradiction or contingency:
[p → (q → r)] ↔ [(p ∧ q) → r]
Determine whether the following statement pattern is a tautology, contradiction or contingency:
[(p ∧ (p → q)] → q
Determine whether the following statement pattern is a tautology, contradiction or contingency:
(p ∧ q) ∨ (∼p ∧ q) ∨ (p ∨ ∼q) ∨ (∼p ∧ ∼q)
Determine whether the following statement pattern is a tautology, contradiction or contingency:
[(p ∨ ∼q) ∨ (∼p ∧ q)] ∧ r
Determine whether the following statement pattern is a tautology, contradiction or contingency:
(p → q) ∨ (q → p)
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∧ q) is T
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∨ q) → q is F
Determine the truth values of p and q in the following case:
(p ∧ q) is F and (p ∧ q) → q is T
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Using truth table, prove the following logical equivalence:
(p ∧ q) → r ≡ p → (q → r)
Using rules in logic, prove the following:
p ↔ q ≡ ∼(p ∧ ∼q) ∧ ∼(q ∧ ∼p)
Using rules in logic, prove the following:
∼p ∧ q ≡ (p ∨ q) ∧ ∼p
Using rules in logic, prove the following:
∼ (p ∨ q) ∨ (∼p ∧ q) ≡ ∼p
Using the rules in logic, write the negation of the following:
(p ∨ q) ∧ (q ∨ ∼r)
Using the rules in logic, write the negation of the following:
p ∧ (q ∨ r)
Using the rules in logic, write the negation of the following:
(p → q) ∧ r
Using the rules in logic, write the negation of the following:
(∼p ∧ q) ∨ (p ∧ ∼q)
Express the following circuit in the symbolic form. Prepare the switching table:
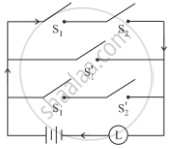
Express the following circuit in the symbolic form. Prepare the switching table:
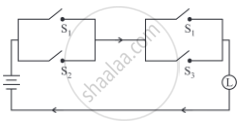
Simplify the following circuit so that the new circuit has minimum number of switches. Also, draw the simplified circuit.
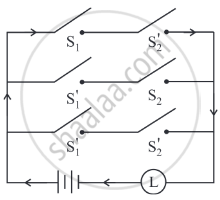
Simplify the following so that the new circuit has a minimum number of switches. Also, draw the simplified circuit.
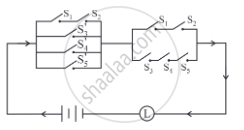
Check whether the following switching circuits are logically equivalent - Justify.
(i)
(ii)

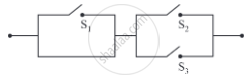
Check whether the following switching circuits are logically equivalent - Justify.
(i)
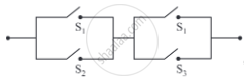
(ii)
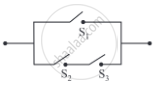
Give alternative arrangement of the switching following circuit, has minimum switches.
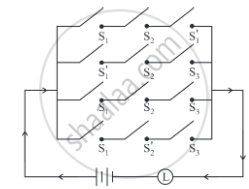
Simplify the following so that the new circuit.
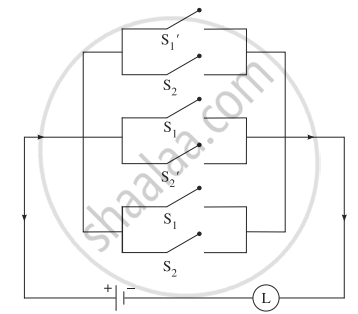
Represent the following switching circuit in symbolic form and construct its switching table. Write your conclusion from the switching table.

Solutions for 1: Mathematical Logic
![Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board chapter 1 - Mathematical Logic Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board chapter 1 - Mathematical Logic - Shaalaa.com](/images/mathematics-and-statistics-1-arts-and-science-english-12-standard-hsc-maharashtra-state-board_6:a050ad90c0124a57a3b775cc0f8ff57b.JPG)
Balbharati solutions for Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board chapter 1 - Mathematical Logic
Shaalaa.com has the Maharashtra State Board Mathematics Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board Maharashtra State Board solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Balbharati solutions for Mathematics Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board Maharashtra State Board 1 (Mathematical Logic) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Balbharati textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board chapter 1 Mathematical Logic are Concept of Statements, Truth Value of Statement, Logical Connective, Simple and Compound Statements, Statement Patterns and Logical Equivalence, Tautology, Contradiction, and Contingency, Duality, Quantifier and Quantified Statements in Logic, Negations of Compound Statements, Converse, Inverse, and Contrapositive, Algebra of Statements, Application of Logic to Switching Circuits.
Using Balbharati Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board solutions Mathematical Logic exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Balbharati Solutions are essential questions that can be asked in the final exam. Maximum Maharashtra State Board Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board students prefer Balbharati Textbook Solutions to score more in exams.
Get the free view of Chapter 1, Mathematical Logic Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board additional questions for Mathematics Mathematics and Statistics 1 (Arts and Science) [English] 12 Standard HSC Maharashtra State Board Maharashtra State Board, and you can use Shaalaa.com to keep it handy for your exam preparation.
