Advertisements
Advertisements
Question
4 × 1023 tritium atoms are contained in a vessel. The half-life of decay tritium nuclei is 12.3 y. Find (a) the activity of the sample, (b) the number of decay in the next 10 hours (c) the number of decays in the next 6.15 y.
Solution
Given:
Number of tritium atoms, N0 = 4 × 1023
Half-life of tritium nuclei, `T_"1/2"`= 12.3 years
Disintegration constant, `lambda = 0.693/T_"1/2" = 0.693/12.3 "years"^-1`
Activity of the sample (A)is given by
`A_0 = "dN"/"dt" = lambdaN_0`
⇒ `A_0 = 0.693/t_"1/2"N_0`
= `0.693/12.3 xx 4 xx 10^23` disintegration/year
= `(0.693 xx 4 xx 10^23)/(12.3 xx 3600 xx 24 xx 365)` disintegration/sec
= `7.146 xx 10^14` disintegration/sec
(b) Activity of the sample, A = 7.146 `xx` 1014 disintegration/sec
Number of decays in the next 10 hours= `7.146 xx 10^14 xx 10 xx 3600`
= `257.256 xx 10^17`
= `2.57 xx 10^19`
(c) Number of atoms left undecayed, N = `N_0e^(-lambdat)`
Here, N0 = Initial number of atoms
`therefore N = 4 xx 10^23 xx e ^((-0.693)/12.3 xx 6.15) = 2.83 xx 10^23`
Number of atoms disintegrated = `(N_0 - N) = (4 - 2.83) xx 10^23 = 1.17 xx 10^23`
APPEARS IN
RELATED QUESTIONS
Write nuclear reaction equation for α-decay of `""_94^242"Pu"`.
Write nuclear reaction equation for β+-decay of `""_43^97"Tc"`.
A radioactive nucleus has a decay constant λ = 0.3465 (day)–1. How long would it take the nucleus to decay to 75% of its initial amount?
Plot a graph showing variation of activity of a given radioactive sample with time.
The sequence of stepwise decay of a radioactive nucleus is
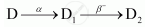
If the atomic number and mass number of D2 are 71 and 176 respectively, what are their corresponding values of D?
The half-life of 199Au is 2.7 days. (a) Find the activity of a sample containing 1.00 µg of 198Au. (b) What will be the activity after 7 days? Take the atomic weight of 198Au to be 198 g mol−1.
Radioactive 131I has a half-life of 8.0 days. A sample containing 131I has activity 20 µCi at t = 0. (a) What is its activity at t = 4 days? (b) What is its decay constant at t = 4.0 days?
A vessel of volume 125 cm3 contains tritium (3H, t1/2 = 12.3 y) at 500 kPa and 300 K. Calculate the activity of the gas.
The count rate of nuclear radiation coming from a radiation coming from a radioactive sample containing 128I varies with time as follows.
| Time t (minute): | 0 | 25 | 50 | 75 | 100 |
| Ctount rate R (109 s−1): | 30 | 16 | 8.0 | 3.8 | 2.0 |
(a) Plot In (R0/R) against t. (b) From the slope of the best straight line through the points, find the decay constant λ. (c) Calculate the half-life t1/2.
A human body excretes (removes by waste discharge, sweating, etc.) certain materials by a law similar to radioactivity. If technetium is injected in some form in a human body, the body excretes half the amount in 24 hours. A patient is given an injection containing 99Tc. This isotope is radioactive with a half-life of 6 hours. The activity from the body just after the injection is 6 μCi. How much time will elapse before the activity falls to 3 μCi?
A charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ. Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
Radioactive isotopes are produced in a nuclear physics experiment at a constant rate dN/dt = R. An inductor of inductance 100 mH, a resistor of resistance 100 Ω and a battery are connected to form a series circuit. The circuit is switched on at the instant the production of radioactive isotope starts. It is found that i/N remains constant in time where i is the current in the circuit at time t and N is the number of active nuclei at time t. Find the half-life of the isotope.
A sample contains a mixture of 108Ag and 110Ag isotopes each having an activity of 8.0 × 108 disintegration per second. 110Ag is known to have larger half-life than 108Ag. The activity A is measured as a function of time and the following data are obtained.
| Time (s) |
Activity (A) (108 disinte- grations s−1) |
Time (s) |
Activity (A 108 disinte-grations s−1) |
| 20 40 60 80 100 |
11.799 9.1680 7.4492 6.2684 5.4115 |
200 300 400 500 |
3.0828 1.8899 1.1671 0.7212 |
(a) Plot ln (A/A0) versus time. (b) See that for large values of time, the plot is nearly linear. Deduce the half-life of 110Ag from this portion of the plot. (c) Use the half-life of 110Ag to calculate the activity corresponding to 108Ag in the first 50 s. (d) Plot In (A/A0) versus time for 108Ag for the first 50 s. (e) Find the half-life of 108Ag.
Copy and complete the following table for a radioactive element whose half-life is 10 minutes. Assume that you have 30g of this element at t = 0.

A radioactive substance decays to 1/16th of its initial mass in 40 days. The half-life of the substance, in days, is:
The half-life of a certain radioactive element is 3.465 days. Find its disintegration constant.
Half-life of a certain radioactive material is 8 hours.
Find the disintegration constant of this material.
