Advertisements
Advertisements
Question
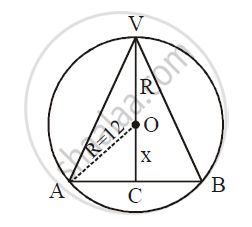
A cone is inscribed in a sphere of radius 12 cm. If the volume of the cone is maximum, find its height
Solution
Let VAB be a cone of greatest volume inscribed in a sphere of radius 12. It is obvious that for
maximum volume the axis of the cone must be along a diameter of the sphere. Let VC be the axis of the cone and O be the centre of the sphere such that OC = x.
Then,
VC = VO + OC = R + x = (12 + x) = height of cone
Applying Pythagoras theorem,
`OA^2 = AC^2 + OC^2`
`AC^2= 12^2 - x^2`
`AC^2 = 144 - x^2`
Let V be the volume of the cone, then
`V = 1/3 pi (AC)^2 (VC)`
`= 1/3pi (144 - x^2) (12 + x)`
`= 1/3 pi [1728 + 144x - 12x^2 - x^3]` .....(i)
`(dV)/dx = 1/3pi [144 - 24x - 3x^2]`
`(d^2V)/(dx^2) = 1/3 pi[-24-6x] = 1/3pi (-6)^2 [4+x]= -2pi(4+x)`
Now, `(dV)/(dx) = 0` given `1/3pi [144 - 24x - 3x^2] = 0`
`i.e. 144 - 24 x - 3x^2 = 0`
i.e `x^2 + 8x - 48 = 0`
i.e (x+12)(x-4) = 0
i.e x = -12 or x = 4
`[(d^2V)/(dx^2)]_(x= 4) = -2pi(4+4) = -16pi <0`
Thus V is maximum when x = 4
Putting x = 4 in (1) we obtain
∴ Height of cone = x + R = 4 + 12 = 16 cm
APPEARS IN
RELATED QUESTIONS
f(x) = 3 + (x − 2)2/3 on [1, 3] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = x2 − 4x + 3 on [1, 3] ?
Verify Rolle's theorem for each of the following function on the indicated interval f (x) = cos 2 (x − π/4) on [0, π/2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = cos 2x on [−π/4, π/4] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = ex cos x on [−π/2, π/2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = cos 2x on [0, π] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = \[\frac{\sin x}{e^x}\] on 0 ≤ x ≤ π ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = \[{e^{1 - x}}^2\] on [−1, 1] ?
At what point on the following curve, is the tangent parallel to x-axis y = x2 on [−2, 2]
?
At what point on the following curve, is the tangent parallel to x-axis y = \[e^{1 - x^2}\] on [−1, 1] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x(x −1) on [1, 2] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 − 3x + 2 on [−1, 2] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 − 2x + 4 on [1, 5] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = x + \frac{1}{x} \text { on }[1, 3]\] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = \sqrt{x^2 - 4} \text { on }[2, 4]\] ?
Find a point on the curve y = x3 + 1 where the tangent is parallel to the chord joining (1, 2) and (3, 28) ?
Let C be a curve defined parametrically as \[x = a \cos^3 \theta, y = a \sin^3 \theta, 0 \leq \theta \leq \frac{\pi}{2}\] . Determine a point P on C, where the tangent to C is parallel to the chord joining the points (a, 0) and (0, a).
Using Lagrange's mean value theorem, prove that (b − a) sec2 a < tan b − tan a < (b − a) sec2 b
where 0 < a < b < \[\frac{\pi}{2}\] ?
If f (x) = Ax2 + Bx + C is such that f (a) = f (b), then write the value of c in Rolle's theorem ?
If the value of c prescribed in Rolle's theorem for the function f (x) = 2x (x − 3)n on the interval \[[0, 2\sqrt{3}] \text { is } \frac{3}{4},\] write the value of n (a positive integer) ?
If from Lagrange's mean value theorem, we have \[f' \left( x_1 \right) = \frac{f' \left( b \right) - f \left( a \right)}{b - a}, \text { then }\]
The value of c in Rolle's theorem for the function \[f\left( x \right) = \frac{x\left( x + 1 \right)}{e^x}\] defined on [−1, 0] is
Find the maximum and minimum values of f(x) = secx + log cos2x, 0 < x < 2π
If the graph of a differentiable function y = f (x) meets the lines y = – 1 and y = 1, then the graph ____________.
It is given that at x = 1, the function x4 - 62x2 + ax + 9 attains its maximum value on the interval [0, 2]. Find the value of a.
If f(x) = ax2 + 6x + 5 attains its maximum value at x = 1, then the value of a is
Let y = `f(x)` be the equation of a curve. Then the equation of tangent at (xo, yo) is :-
