Advertisements
Advertisements
Question
A fruit grower can use two types of fertilizer in his garden, brand P and Q. The amounts (in kg) of nirogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicates that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
| kg per bag | ||
| Brand P | Brand P | |
| Nitrogen | 3 | 3.5 |
| Phosphoric acid | 1 | 2 |
| Potash | 3 | 1.5 |
| Chlorine | 1.5 | 2 |
If the grower wants to minimize the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
Solution
Let x bags of fertilizer of brand P and y bags of fertilizer of brand Q are used in the garden.
One bag of brand P contains 3 kg of nitrogen and one bag of brand Q contains 3.5 kg of nitrogen, therefore, x bags of brand P and y bags of brand Q will contain (3x + 3.5y) kg of nitrogen.
Since one bag of brand P contains 1 kg of phosphoric acid and one bag of brand Q contains 2 kg of phosphoric acid, therefore, x bags of brand P and y bags of brand Q will contain (x + 2y) kg of phosphoric acid. But, the garden needs at least 240 kg of phosphoric acid.
∴ x + 2y ≥ 240
Similarly, x bags of brand P and y bags of brand Q will contain (3x + 1.5y) kg of potash. But, the garden needs at least 270 kg of potash.
∴ 3x + 1.5y ≥ 270
⇒ 2x + y ≥ 180
Also, x bags of brand P and y bags of brand Q will contain (1.5x + 2y) kg of chlorine. But, the garden needs at most 310 kg of chlorine.
∴ 1.5x + 2y ≤ 310
Thus, the given linear programming problem is
Minimise Z = 3x + 3.5y
subject to the constraints
x + 2y ≥ 240
2x + y ≥ 180
1.5x + 2y ≤ 310
x, y ≥ 0
The feasible region determined by the given constraints can be diagrammatically represented as,
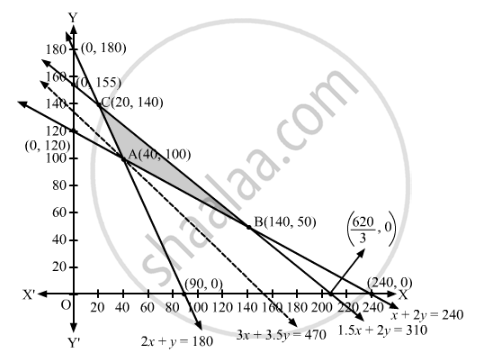
The coordinates of the corner points of the feasible region are A(40, 100), B(140, 50) and C(20, 140).
The value of the objective function at these points are given in the following table.
| Corner Point | Z = 3x + 3.5y |
| (40, 100) | 3 × 40 + 3.5 × 100 = 470 → Minimum |
| (140, 50) | 3 × 140 + 3.5 × 50 = 595 |
| (20, 140) | 3 × 20 + 3.5 × 140 = 550 |
The smallest value of Z is 470 which is obtained at (40, 100).
It can be seen that the open half-plane represented by 3x + 3.5y < 470 has no common points with the feasible region.
So, the minimum value of Z is 470.
Hence, 40 bags of fertilizer of brand P and 100 bags of fertilizer of brand Q are used in the garden. The minimum amount of nitrogen added in the garden is 470 kg.
APPEARS IN
RELATED QUESTIONS
Minimize `z=4x+5y ` subject to `2x+y>=7, 2x+3y<=15, x<=3,x>=0, y>=0` solve using graphical method.
A dealer in rural area wishes to purchase a number of sewing machines. He has only Rs 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him Rs 360 and a manually operated sewing machine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a manually operated sewing machine at a profit of Rs 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0 and x, y ≥ 0
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = 15x + 10y
Subject to
\[3x + 2y \leq 80\]
\[2x + 3y \leq 70\]
\[ x, y \geq 0\]
Maximize Z = 3x + 4y
Subject to
\[2x + 2y \leq 80\]
\[2x + 4y \leq 120\]
Maximize Z = 7x + 10y
Subject to
\[x + y \leq 30000\]
\[ y \leq 12000\]
\[ x \geq 6000\]
\[ x \geq y\]
\[ x, y \geq 0\]
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Show the solution zone of the following inequalities on a graph paper:
\[5x + y \geq 10\]
\[ x + y \geq 6\]
\[x + 4y \geq 12\]
\[x \geq 0, y \geq 0\]
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
Solve the following linear programming problem graphically:
Minimize z = 6 x + 3 y
Subject to the constraints:
4 x + \[y \geq\] 80
x + 5 \[y \geq\] 115
3 x + 2 \[y \leq\] 150
\[x \geq\] 0 , \[y \geq\] 0
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 of calories. Two foods A and B, are available at a cost of Rs 4 and Rs 3 per unit respectively. If one unit of A contains 200 units of vitamin, 1 unit of mineral and 40 calories and one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 calories, find what combination of foods should be used to have the least cost?
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2 are available. Food F1 costs Rs 4 per unit and F2 costs Rs 6 per unit one unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these foods and also meets the mineral nutritional requirements
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum of vitamin A.
A company produces two types of leather belts, say type A and B. Belt A is a superior quality and belt B is of a lower quality. Profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Each belt of type A requires twice as much time as required by a belt of type B. If all belts were of type B, the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day (both A and B combined). Belt A requires a fancy buckle and only 400 fancy buckles are available for this per day. For belt of type B, only 700 buckles are available per day.
How should the company manufacture the two types of belts in order to have a maximum overall profit?
A manufacturer makes two types A and B of tea-cups. Three machines are needed for the manufacture and the time in minutes required for each cup on the machines is given below:
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise, show that 15 tea-cups of type A and 30 of type B should be manufactured in a day to get the maximum profit.
A publisher sells a hard cover edition of a text book for Rs 72.00 and paperback edition of the same ext for Rs 40.00. Costs to the publisher are Rs 56.00 and Rs 28.00 per book respectively in addition to weekly costs of Rs 9600.00. Both types require 5 minutes of printing time, although hardcover requires 10 minutes binding time and the paperback requires only 2 minutes. Both the printing and binding operations have 4,800 minutes available each week. How many of each type of book should be produced in order to maximize profit?
A man owns a field of area 1000 sq.m. He wants to plant fruit trees in it. He has a sum of Rs 1400 to purchase young trees. He has the choice of two types of trees. Type A requires 10 sq.m of ground per tree and costs Rs 20 per tree and type B requires 20 sq.m of ground per tree and costs Rs 25 per tree. When fully grown, type A produces an average of 20 kg of fruit which can be sold at a profit of Rs 2.00 per kg and type B produces an average of 40 kg of fruit which can be sold at a profit of Rs. 1.50 per kg. How many of each type should be planted to achieve maximum profit when the trees are fully grown? What is the maximum profit?
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
A manufacturer has three machine I, II, III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines.
The number of hours required for producing 1 unit each of M and N on the three machines are given in the following table:
| Items | Number of hours required on machines | ||
| I | II | III | |
| M | 1 | 2 | 1 |
| N | 2 | 1 | 1.25 |
She makes a profit of ₹600 and ₹400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
The graph of the inequality 3X − 4Y ≤ 12, X ≤ 1, X ≥ 0, Y ≥ 0 lies in fully in
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
The constraints of an LPP are 7 ≤ x ≤ 12, 8 ≤ y ≤ 13. Determine the vertices of the feasible region formed by them.
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is ______.
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
In linear programming feasible region (or solution region) for the problem is ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is ____________.
Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to x + y ≤ 200, x ≤ 40, x ≥ 20, y ≥ 0
The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
The corner points of the feasible region of a linear programming problem are (0, 4), (8, 0) and `(20/3, 4/3)`. If Z = 30x + 24y is the objective function, then (maximum value of Z – minimum value of Z) is equal to ______.
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
