Advertisements
Advertisements
Question
A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
Solution
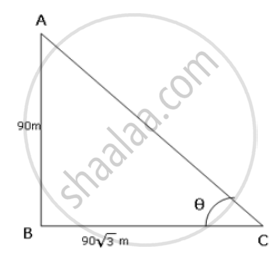
Let AB be the pole and BC be its shadow.
In ΔABC,
tanθ = `"AB"/"BC"`
⇒ `tanθ = 90/(90sqrt(3)) = 1/sqrt(3)`
But, `tan30^circ = 1/sqrt(3)`
∴ `θ = 30^circ`
Thus , the angle of elevation is `30^circ`.
APPEARS IN
RELATED QUESTIONS
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
