Advertisements
Advertisements
Question
ABCD is a parallelogram, AD is produced to E so that DE = DC and EC produced meets AB produced in F. Prove that BF = BC.
Solution
Draw a parallelogram ABCD with AC and BD intersecting at O
Produce AD to E such that DE = DC
Join EC and produce it to meet AB produced at F.
In ΔDCE ,
∴`∠`DCE = `∠`DEC .........CD [In a triangle, equal sides have equal angles opposite]
AB || CD (Opposite sides of the parallelogram are parallel)
∴AE || CD ( AB Lies on AF )
AF || CD and EF is the transversal.
∴`∠`DCE = `∠`BFC .....(2) [Pair of corresponding angles]
From (1) and (2), we get
`∠`DEC = `∠`BFC
In ΔAFE,
`∠`AFE = `∠`AEF (`∠`DEC = `∠`BFC )
∴AE = AF (In a triangle, equal angles have equal sides opposite to them)
⇒ AD + DE = AB + BF
⇒ BC + AB = AB + BF [ ∵ AD = BC, DE = CD and CD = AB, AB = DE ]
⇒ BC = BF
APPEARS IN
RELATED QUESTIONS
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
In an isosceles trapezium one pair of opposite sides are _____ to each Other and the other pair of opposite sides are _____ to each other.
A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is ______.
What is the maximum number of obtuse angles that a quadrilateral can have?
If a bicycle wheel has 48 spokes, then the angle between a pair of two consecutive spokes is ______.
In figure, ∠XYZ cannot be written as ______.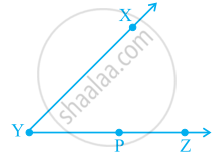
The number of obtuse angles in figure is ______.
In given figure, name any two angles that appear to be obtuse angles.
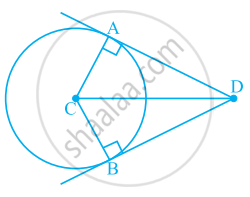
Using the information given, name the right angles in part of figure:
RT ⊥ ST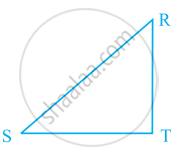
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?