Advertisements
Advertisements
Question
Answer the following:
R = {1, 2, 3} → {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} Check if R is transitive
Solution
∴ (1, 2), (2, 3) ∈ R but (1, 3) ∉ R
∴ R is not transitive
APPEARS IN
RELATED QUESTIONS
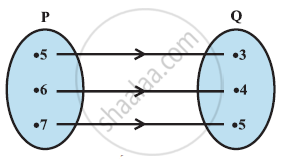
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
If A = [1, 2, 3], B = [4, 5, 6], which of the following are relations from A to B? Give reasons in support of your answer.
(i) [(1, 6), (3, 4), (5, 2)]
(ii) [(1, 5), (2, 6), (3, 4), (3, 6)]
(iii) [(4, 2), (4, 3), (5, 1)]
(iv) A × B.
Find the inverse relation R−1 in each of the cases:
(ii) R = {(x, y), : x, y ∈ N, x + 2y = 8}
Find the inverse relation R−1 in each of the cases:
(iii) R is a relation from {11, 12, 13} to (8, 10, 12] defined by y = x − 3.
Let A = (3, 5) and B = (7, 11). Let R = {(a, b) : a ∈ A, b ∈ B, a − b is odd}. Show that R is an empty relation from A into B.
Let A = [1, 2] and B = [3, 4]. Find the total number of relation from A into B.
Determine the domain and range of the relation R defined by
(i) R = [(x, x + 5): x ∈ (0, 1, 2, 3, 4, 5)]
Determine the domain and range of the relation R defined by
(ii) R = {(x, x3) : x is a prime number less than 10}
Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b2}. Is the statement true?
(a, b) ∈ R implies (b, a) ∈ R
Justify your answer in case.
If R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4} is a relation defined on the set Z of integers, then write domain of R.
If R is a relation on the set A = [1, 2, 3, 4, 5, 6, 7, 8, 9] given by x R y ⇔ y = 3x, then R =
A relation ϕ from C to R is defined by x ϕ y ⇔ |x| = y. Which one is correct?
If the set A has p elements, B has q elements, then the number of elements in A × B is
If R is a relation from a finite set A having m elements of a finite set B having n elements, then the number of relations from A to B is
If R is a relation on a finite set having n elements, then the number of relations on A is
Write the relation in the Roster Form. State its domain and range
R2 = `{("a", 1/"a") // 0 < "a" ≤ 5, "a" ∈ "N"}`
Write the relation in the Roster Form. State its domain and range
R6 = {(a, b)/a ∈ N, a < 6 and b = 4}
Select the correct answer from given alternative.
If (x, y) ∈ R × R, then xy = x2 is a relation which is
Answer the following:
Determine the domain and range of the following relation.
R = {(a, b)/b = |a – 1|, a ∈ Z, IaI < 3}
Answer the following:
Find R : A → A when A = {1, 2, 3, 4} such that R = {(a, b)/|a − b| ≥ 0}
Answer the following:
Show that the following is an equivalence relation
R in A is set of all books. given by R = {(x, y)/x and y have same number of pages}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R2 = {(–1, 1)}
A company has four categories of employees given by Assistants (A), Clerks (C), Managers (M), and an Executive Officer (E). The company provides ₹ 10,000, ₹ 25,000, ₹ 50,000, and ₹ 1,00,000 as salaries to the people who work in the categories A, C, M, and E respectively. If A1, A2, A3, A4, and A5 were Assistants; C1, C2, C3, C4 were Clerks; M1, M2, M3 were managers and E1, E2 was Executive officers and if the relation R is defined by xRy, where x is the salary given to person y, express the relation R through an ordered pair and an arrow diagram
Let A = {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f : A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f
Find the domain of the function f(x) = `sqrt(1 + sqrt(1 - sqrt(1 - x^2)`
Discuss the following relation for reflexivity, symmetricity and transitivity:
The relation R defined on the set of all positive integers by “mRn if m divides n”
Discuss the following relation for reflexivity, symmetricity and transitivity:
Let P denote the set of all straight lines in a plane. The relation R defined by “lRm if l is perpendicular to m”
Discuss the following relation for reflexivity, symmetricity and transitivity:
Let A be the set consisting of all the female members of a family. The relation R defined by “aRb if a is not a sister of b”
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it symmetric
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is equivalence
Prove that the relation “friendship” is not an equivalence relation on the set of all people in Chennai
Is the following relation a function? Justify your answer
R1 = `{(2, 3), (1/2, 0), (2, 7), (-4, 6)}`
Given R = {(x, y) : x, y ∈ W, x2 + y2 = 25}. Find the domain and Range of R.
Is the given relation a function? Give reasons for your answer.
t = {(x, 3) | x is a real number
Let S = {x ∈ R : x ≥ 0 and `2|sqrt(x) - 3| + sqrt(x)(sqrt(x) - 6) + 6 = 0}`. Then S ______.
A relation on the set A = {x : |x| < 3, x ∈ Z}, where Z is the set of integers is defined by R = {(x, y) : y = |x| ≠ –1}. Then the number of elements in the power set of R is ______.
