Advertisements
Advertisements
Question
Consider the situation shown in figure . Show that if the blocks are displaced slightly in opposite direction and released, they will execute simple harmonic motion. Calculate the time period.
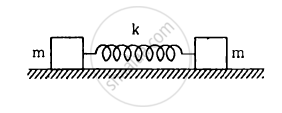
Solution
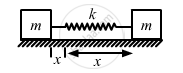
The centre of mass of the system should not change during simple harmonic motion.
Therefore, if the block m on the left hand side moves towards right by distance x, the block on the right hand side should also move towards left by distance x. The total compression of the spring is 2x.
If v is the velocity of the block. Then
Using energy method, we can write:
\[\frac{1}{2}k \left( 2x \right)^2 + \frac{1}{2}m v^2 + \frac{1}{2}m v^2 = C\]
⇒ mv2 + 2kx2 = C
By taking the derivative of both sides with respect to t, we get:
\[2mv\frac{dv}{dt} + 2k \times 2x\frac{dx}{dt} = 0\]
\[\text { Putting } v = \frac{dx}{dt}; \text { and } a = \frac{dv}{dt}\text { in above expression, we get }\]
\[ ma + 2kx = 0 \]
\[ \Rightarrow - \frac{a}{x} = \frac{2k}{m} = \omega^2 \]
\[ \Rightarrow \omega = \sqrt{\frac{2k}{m}}\]
\[ \Rightarrow \text { Time period }, T = 2\pi\sqrt{\left( \frac{m}{2k} \right)}\]
APPEARS IN
RELATED QUESTIONS
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A,
(b) at the end B,
(c) at the mid-point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and
(f) at 4 cm away from B going towards A.
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
A block suspended from a vertical spring is in equilibrium. Show that the extension of the spring equals the length of an equivalent simple pendulum, i.e., a pendulum having frequency same as that of the block.
A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314 s. Find the maximum force exerted by the spring on the block.
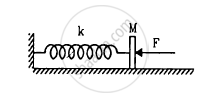
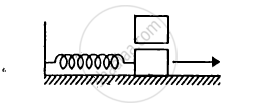
In following figure k = 100 N/m M = 1 kg and F = 10 N.
- Find the compression of the spring in the equilibrium position.
- A sharp blow by some external agent imparts a speed of 2 m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
- Find the time period of the resulting simple harmonic motion.
- Find the amplitude.
- Write the potential energy of the spring when the block is at the left extreme.
- Write the potential energy of the spring when the block is at the right extreme.
The answer of b, e and f are different. Explain why this does not violate the principle of conservation of energy.
Repeat the previous exercise if the angle between each pair of springs is 120° initially.
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.
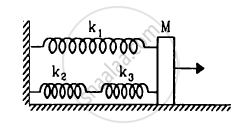
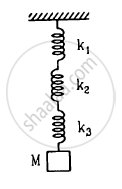
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
A 1 kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N/m. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.
Find the elastic potential energy stored in each spring shown in figure when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
Discuss in detail the energy in simple harmonic motion.
When a particle executing S.H.M oscillates with a frequency v, then the kinetic energy of the particle?
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Draw a graph to show the variation of P.E., K.E. and total energy of a simple harmonic oscillator with displacement.
Find the displacement of a simple harmonic oscillator at which its P.E. is half of the maximum energy of the oscillator.
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
What is the amplitude of oscillation?
