Advertisements
Advertisements
Question
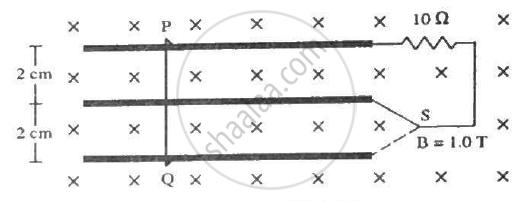
Consider the situation shown in figure. The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5 cm s−1. Find the current in the 10 Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.
Solution
Given:-
Magnetic field, B = 1 T
Velocity of the sliding wire, v = 5 × 10−2 m/s
Resistance of the connected resistor, R = 10 Ω
(a) When the switch is thrown to the middle rail:-
Length of the sliding wire = 2 × 10−2 m
Induced emf, E = Bvl
= 1 × (5 × 10−2) × (2 × 10−2) V
= 10 × 10−4 = 10−3 V
Current in the 10 Ω resistor is given by
\[i = \frac{E}{R}\]
\[ = \frac{{10}^{- 3}}{10} = {10}^{- 4} = 0 . 1 mA\]
(b) When the switch is thrown to the bottom rail:-
The length of the sliding wire becomes 4 × 10−2 m.
The induced emf is given by
E = Bvl'
= 1 × (5 × 10−2) × (4 × 10−2)
= 20 × 10−4 V
Now,
Current, \[i = \frac{20 \times {10}^{- 4}}{10}A\]
= 2 × 10−4 A = 0.2 mA
APPEARS IN
RELATED QUESTIONS
The current flowing through an inductor of self-inductance L is continuously increasing. Plot a graph showing the variation of
Induced emf versus dI/dt
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

What is motional emf? State any two factors on which it depends.
A metallic rod of length ‘l’ is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present everywhere. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtained the expression for it.
Consider the following statements:-
(A) An emf can be induced by moving a conductor in a magnetic field.
(B) An emf can be induced by changing the magnetic field.
Consider the situation shown in figure. The wire AB is slid on the fixed rails with a constant velocity. If the wire AB is replaced by a semicircular wire, the magnitude of the induced current will _____________ .

A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
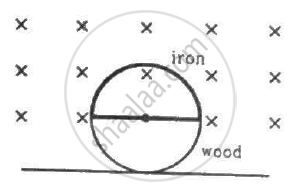
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
A metallic metre stick moves with a velocity of 2 m s−1 in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf induced between the ends of the stick.
A 10 m wide spacecraft moves through the interstellar space at a speed 3 × 107 m s−1. A magnetic field B = 3 × 10−10 T exists in the space in a direction perpendicular to the plane of motion. Treating the spacecraft as a conductor, calculate the emf induced across its width.
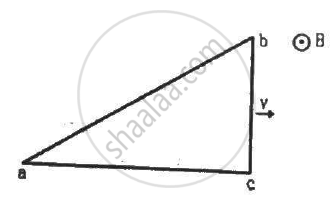
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular to the diameter joining free ends, (b) the velocity is parallel to this diameter.
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
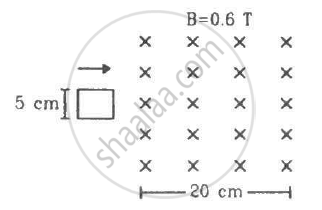
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the total heat produced in the loop during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.
A rod of length l rotates with a uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is ___________ .
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
An induced e.m.f. is produced when a magnet is plunged into a coil. The strength of the induced e.m.f. is independent of ______.
In the given figure current from A to B in the straight wire is decreasing. The direction of induced current in the loop is A ______.