Advertisements
Advertisements
Question
Derive the equation for acceptance angle and numerical aperture, of optical fiber.
Solution
- To ensure the critical angle incident in the core-cladding boundary inside the optical fibre, the light should be incident at a certain angle at the end of the optical fiber while entering into it. This angle is called an acceptance angle.
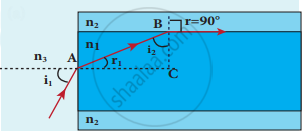
acceptance angle
acceptance cone - By Snell’s law
n3 sin ia = n1 sin ra
To have the internal reflection inside optical fibre,
n1 sin i1 = n2 sin 90°
n1 sin ic = n2 sin 90° = 1
∴ sin ic = `"n"_2/"n"_1` - From the right angle triangle AABC,
ic = 90° – ra
Now, equation becomes
sin (90° – ra) = `"n"_2/"n"_1` - Using trigonometry,
cos ra = `"n"_2/"n"_1`
sin ra = `sqrt(1 - cos^2 "r"_"a")`
Substituting for cos ra
sin ra = `sqrt(1 - ("n"_2/"n"_1)^2) = sqrt(("n"_1^2 - "n"_2^2)/"n"_1^2)`
Substituting this in equation (1)
n3 sin ia = `"n"_1 sqrt(("n"_1^2 - "n"_2^2)/"n"_1^2) = sqrt("n"_1^2 - "n"_2^2)`
On further simplification,
sin ia = `sqrt(("n"_1^2 - "n"_2^2)/"n"_3)` or sin ia = `sqrt(("n"_1^2 - "n"_2^2)/"n"_3)`
`"i"_"a" = sin^-1 (sqrt(("n"_1^2 - "n"_2^2)/"n"_3))`
If outer medium is air, then n3 = 1. The acceptance angle ia becomes,
`"i"_"a" = sin^-1 (sqrt("n"_1^2 - "n"_2^2))` - Light can have any angle of incidence from o to ia with the normal at the end of the optical fibre forming a conical shape called acceptance cone.
The term (n3 sin ia) is called numerical aperture NA of the optical fibre
NA = n3 sin ia = `sqrt("n"_1^2 - "n"_2^2)` - 6. If outer medium is air, then n3 = 1. The numeric aperture NA becomes,
NA = sin ia = `sqrt("n"_1^2 - "n"_2^2)`
APPEARS IN
RELATED QUESTIONS
Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?
A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1·6. If it is immersed in a liquid of refractive index 1·3, find its new focal length.
Is the formula "Real depth/Apparent depth = μ" valid if viewed from a position quite away from the normal?
A narrow beam of white light goes through a slab having parallel faces.
(a) The light never splits in different colours
(b) The emergent beam is white
(c) The light inside the slab is split into different colours
(d) The light inside the slab is white
A convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 10 cm apart with their principal axes coinciding. A beam of light travelling parallel to the principal axis and having a beam diameter 5.0 mm, is incident on the combination. Show that the emergent beam is parallel to the incident one. Find the beam diameter of the emergent beam.
Stars twinkle due to ______.
Obtain the equation for critical angle.
What is Snell’s window?
Obtain the equation for radius of illumination (or) Snell’s window.
A beam of light travels from air into a medium. Its speed and wavelength in the medium are 1.5 × 108 ms-1 and 230 nm respectively. The wavelength of light in the air will be ______.
