Question

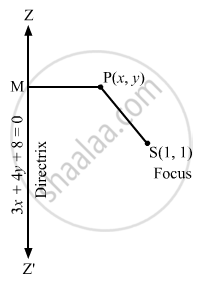
Find the equation of the hyperbola whose focus is (1, 1), directrix is 3x + 4y + 8 = 0 and eccentricity = 2 .

Answer 1

Let S be the focus and  \[P\left( x, y \right)\] be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM

\[\Rightarrow\] \[\sqrt{(x - 1 )^2 + (y - 1 )^2} = 2\left( \frac{3x + 4y + 8}{5} \right)\]

Squaring both the sides:

\[(x - 1 )^2 + (y - 1 )^2 = 4 \left( \frac{3x + 4y + 8}{5} \right)^2 \]

\[ \Rightarrow x^2 + 1 - 2x + y^2 + 1 - 2y = \frac{4}{25}\left( 9 x^2 + 16 y^2 + 64 + 24xy + 64y + 48x \right)\]

\[ \Rightarrow 25 x^2 + 25 - 50x + 25 y^2 + 25 - 50y = 36 x^2 + 64 y^2 + 256 + 96xy + 256y + 192x\]

\[ \Rightarrow 11 x^2 + 39 y^2 + 96xy + 306y + 242x + 206 = 0\]

∴ Equation of the hyperbola = \[11 x^2 + 39 y^2 + 96xy + 306y + 242x + 206 = 0\]