Question

Find the equation of the parabola whose focus is (5, 2) and having vertex at (3, 2). 

Answer 1

Given:
The vertex and the focus of the parabola are (3, 2) and (5, 2), respectively.

∴ Slope of the axis of the parabola = 0

 Slope of the directrix cannot be defined.

Let the directrix intersect the axis at K (r, s). 

∴ \[\frac{r + 5}{2} = 3, \frac{s + 2}{2} = 2\]
\[ \Rightarrow r = 1, s = 2\] 

Required equation of the directrix is \[x - 1 = 0\] 

which can be rewritten as x = 1.

Let P (x, y) be any point on the parabola whose focus is S (5, 2) and the directrix is x =1

 

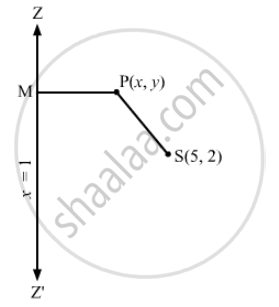
Draw PM perpendicular to x  = 1.
Then, we have: \[SP = PM\]
\[ \Rightarrow S P^2 = P M^2 \]
\[ \Rightarrow \left( x - 5 \right)^2 + \left( y - 2 \right)^2 = \left( \frac{x - 1}{1} \right)^2 \]
\[ \Rightarrow x^2 + 25 - 10x + y^2 + 4 - 4y = x^2 + 1 - 2x\]
\[ \Rightarrow 25 - 10x + y^2 + 4 - 4y - 1 + 2x = 0\]
\[ \Rightarrow y^2 - 4y - 8x + 28 = 0\]