Advertisements
Advertisements
Question
An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?
Solution
Its form is of the shape of a parabola.
Let OX, OY be its coordinate axis, and the equation is y2 = 4ax.
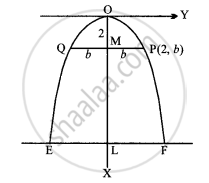
Height of arch, OL = 10 m
Width EF = 5 m
LF = `1/2` EF = `1/2 xx 5 = 5/2`
Coordinates of point F `(10, 5/2)`
Since the point `(10, 5/2)` lies on the parabola y2 = 4ax
∴ `(5/2)^2 = 4a xx 10` or `40a = 25/4`
∴ 4a = `25/4 xx 1/10 = 5/8`
∴ Equation of parabola y2 = `5/8 x`
2 m below top O, let the width of the arch be 2b.
∴ PM = `1/2 "PQ" = 1/2 xx 2"b" = "b"`
P has coordinates of the point (2, b) which lies on the parabola `"y"^2 = 5/8 "x"`.
∴ `"b"^2 = 5/8 xx 2 = 5/4`
∴ b = `sqrt5/2`
The width of the arch at this location,
= `2"b"`
= `2 xx sqrt5/2`
= `sqrt5` meter
= 2.24 meters (approximately)
APPEARS IN
RELATED QUESTIONS
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
An equilateral triangle is inscribed in the parabola y2 = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
Find the equation of the parabola whose:
focus is (3, 0) and the directrix is 3x + 4y = 1
Find the equation of the parabola whose:
focus is (0, 0) and the directrix 2x − y − 1 = 0
Find the equation of the parabola whose:
focus is (2, 3) and the directrix x − 4y + 3 = 0.
Find the equation of the parabola whose focus is the point (2, 3) and directrix is the line x − 4y + 3 = 0. Also, find the length of its latus-rectum.
Find the equation of the parabola if
the focus is at (−6, −6) and the vertex is at (−2, 2)
Find the equation of the parabola if
the focus is at (0, −3) and the vertex is at (0, 0)
Find the equation of the parabola if the focus is at (0, −3) and the vertex is at (−1, −3)
At what point of the parabola x2 = 9y is the abscissa three times that of ordinate?
Find the equation of a parabola with vertex at the origin, the axis along x-axis and passing through (2, 3).
Find the equation of the parabola whose focus is (5, 2) and having vertex at (3, 2).
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest wire being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
Find the coordinates of points on the parabola y2 = 8x whose focal distance is 4.
If the points (0, 4) and (0, 2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
Write the equation of the directrix of the parabola x2 − 4x − 8y + 12 = 0.
Write the equation of the parabola whose vertex is at (−3,0) and the directrix is x + 5 = 0.
The equation of the parabola whose vertex is (a, 0) and the directrix has the equation x + y = 3a, is
The parametric equations of a parabola are x = t2 + 1, y = 2t + 1. The cartesian equation of its directrix is
The equation 16x2 + y2 + 8xy − 74x − 78y + 212 = 0 represents
If the coordinates of the vertex and the focus of a parabola are (−1, 1) and (2, 3) respectively, then the equation of its directrix is
The locus of the points of trisection of the double ordinates of a parabola is a
The equations of the lines joining the vertex of the parabola y2 = 6x to the points on it which have abscissa 24 are ______.
The equation of the parabola whose focus is the point (2, 3) and directrix is the line x – 4y + 3 = 0 is ______.
Find the coordinates of a point on the parabola y2 = 8x whose focal distance is 4.
Find the length of the line segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line segment makes an angle θ to the x-axis.
If the line y = mx + 1 is tangent to the parabola y2 = 4x then find the value of m.
Find the equation of the set of all points whose distance from (0, 4) are `2/3` of their distance from the line y = 9.
The line lx + my + n = 0 will touch the parabola y2 = 4ax if ln = am2.
If the focus of a parabola is (0, –3) and its directrix is y = 3, then its equation is ______.
If the vertex of the parabola is the point (–3, 0) and the directrix is the line x + 5 = 0, then its equation is ______.
