Advertisements
Advertisements
Question
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.
Solution
The diameter of the parabolic reflector, AOB,
AB = 20 cm
and AM = 10 cm
deep of reflector, OM = 5 cm
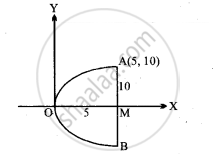
If OX, OY are the coordinate axis then the point lies on the parabola.
Let the equation of parabola be, y2 = 4ax
∴ 102 = 4a × 5
= 100 = 20a
a = `100/20`
∴ a = 5
The focus of the parabola is (a, 0) or (5, 0).
APPEARS IN
RELATED QUESTIONS
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
x2 = 6y
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
y2 = – 8x
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0); focus (3, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) focus (–2, 0)
An equilateral triangle is inscribed in the parabola y2 = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
Find the equation of the parabola whose:
focus is (3, 0) and the directrix is 3x + 4y = 1
Find the equation of the parabola whose:
focus is (0, 0) and the directrix 2x − y − 1 = 0
Find the equation of the parabola if
the focus is at (0, −3) and the vertex is at (0, 0)
Find the equation of the parabola if the focus is at (0, −3) and the vertex is at (−1, −3)
Find the equation of the parabola if the focus is at (a, 0) and the vertex is at (a', 0)
Find the equation of a parabola with vertex at the origin, the axis along x-axis and passing through (2, 3).
Find the equation of the parabola whose focus is (5, 2) and having vertex at (3, 2).
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest wire being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
Find the equations of the lines joining the vertex of the parabola y2 = 6x to the point on it which have abscissa 24.
Find the coordinates of points on the parabola y2 = 8x whose focal distance is 4.
If the line y = mx + 1 is tangent to the parabola y2 = 4x, then find the value of m.
Write the equation of the parabola whose vertex is at (−3,0) and the directrix is x + 5 = 0.
The equation of the parabola whose vertex is (a, 0) and the directrix has the equation x + y = 3a, is
The parametric equations of a parabola are x = t2 + 1, y = 2t + 1. The cartesian equation of its directrix is
The line 2x − y + 4 = 0 cuts the parabola y2 = 8x in P and Q. The mid-point of PQ is
If the coordinates of the vertex and the focus of a parabola are (−1, 1) and (2, 3) respectively, then the equation of its directrix is
The locus of the points of trisection of the double ordinates of a parabola is a
The equation of the directrix of the parabola whose vertex and focus are (1, 4) and (2, 6) respectively is
If V and S are respectively the vertex and focus of the parabola y2 + 6y + 2x + 5 = 0, then SV =
The equation of the parabola whose focus is (1, −1) and the directrix is x + y + 7 = 0 is
Find the coordinates of a point on the parabola y2 = 8x whose focal distance is 4.
Find the equation of the following parabolas:
Directrix x = 0, focus at (6, 0)
Find the equation of the following parabolas:
Focus at (–1, –2), directrix x – 2y + 3 = 0
Find the equation of the set of all points the sum of whose distances from the points (3, 0) and (9, 0) is 12.
If the focus of a parabola is (0, –3) and its directrix is y = 3, then its equation is ______.
If the vertex of the parabola is the point (–3, 0) and the directrix is the line x + 5 = 0, then its equation is ______.
The equation of the ellipse whose focus is (1, –1), the directrix the line x – y – 3 = 0 and eccentricity `1/2` is ______.
