Advertisements
Advertisements
Question
Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and (6, 0, 0).
Solution
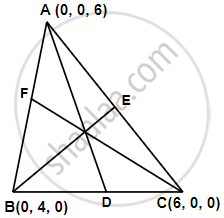
The midpoint of the line segment joining the points B(0, 4, 0) and C(6, 0, 0) is D `((0 + 6)/2, (4 + 0)/2, (0 + 0)/ 2)` or (3, 2, 0).
The coordinates of point A are (0, 0, 6).
Length of median AD of triangle ABC
= `sqrt((3 - 0)^2 + (2 - 0)^2 + (0 - 6)^2)`
= `sqrt(9 + 4 + 36)`
= `sqrt49`
= 7
The coordinates of C and A are (6, 0, 0) and (0, 0, 6)
The mid-point of AC is E `((0 + 6)/2, (0 + 0)/2, (0 + 6)/2)` or E (3, 0, 3)
And coordinates of B are (0, 4, 0).
Length of median BE of triangle ABC
= `sqrt((3 - 0)^2 + (0 - 4)^2 + (3 - 0)^2)`
= `sqrt(9 + 16 + 9)`
= `sqrt34`
The coordinates of points A and B are (0, 0, 6), (0, 4, 0) respectively.
∴ The midpoint of AB is F`((0 + 0)/2, (0 + 4)/2, (6 + 0)/2)` or F (0, 2, 3).
Length of median CF of triangle ABC
= `sqrt((6 - 0)^2 + (0 - 2)^2 + (0 + 3)^2)`
= `sqrt(36 + 4 + 9)`
= `sqrt49`
= 7
APPEARS IN
RELATED QUESTIONS
A point is in the XZ-plane. What can you say about its y-coordinate?
The coordinates of points in the XY-plane are of the form _______.
Find the coordinates of a point on y-axis which are at a distance of `5sqrt2` from the point P (3, –2, 5).
A point R with x-coordinate 4 lies on the line segment joining the pointsP (2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint suppose R divides PQ in the ratio k: 1. The coordinates of the point R are given by `((8k + 2)/(k+1), (-3)/(k+1), (10k + 4)/(k+1))`
If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.
A(1, 2, 3), B(0, 4, 1), C(–1, –1, –3) are the vertices of a triangle ABC. Find the point in which the bisector of the angle ∠BAC meets BC.
Find the coordinates of the points which tisect the line segment joining the points P(4, 2, –6) and Q(10, –16, 6).
Given that P(3, 2, –4), Q(5, 4, –6) and R(9, 8, –10) are collinear. Find the ratio in which Qdivides PR.
Find the ratio in which the line segment joining the points (4, 8, 10) and (6, 10, –8) is divided by the yz-plane.
Find the coordinates of a point equidistant from the origin and points A (a, 0, 0), B (0, b, 0) andC(0, 0, c).
Write the coordinates of the point P which is five-sixth of the way from A(−2, 0, 6) to B(10, −6, −12).
If a parallelopiped is formed by the planes drawn through the points (2,3,5) and (5, 9, 7) parallel to the coordinate planes, then write the lengths of edges of the parallelopiped and length of the diagonal.
Determine the point on yz-plane which is equidistant from points A(2, 0, 3), B(0, 3,2) and C(0, 0,1).
If the origin is the centroid of a triangle ABC having vertices A(a, 1, 3), B(−2, b −5) and C (4, 7, c), find the values of a, b, c.
P is a point on the line segment joining the points (3, 2, –1) and (6, 2, –2). If x co-ordinate of P is 5, then its y co-ordinate is ______.
The equations of x-axis in space are ______.
The points (1, 2, 3), (–2, 3, 4) and (7, 0, 1) are collinear.
The vector equation of the line passing through the points (3, 5, 4) and (5, 8, 11) is.
Find the position vector of a point A in space such that `vec(OA)` is inclined at 60º to OX and at 45° to OY and `|vec(OA)|` = 10 units
Find the vector equation of the line which is parallel to the vector `3hati - 2hatj + 6hatk` and which passes through the point (1 ,–2, 3).
Show that the lines `(x - 1)/2 = (y - 2)/3 = (z - 3)/4` and `(x - 4)/5 = (y - 1)/2` = z intersect.. Also, find their point of intersection.
The reflection of the point (α, β, γ) in the xy-plane is ______.
A plane passes through the points (2, 0, 0) (0, 3, 0) and (0, 0, 4). The equation of plane is ______.
The equation of a line, which is parallel to `2hati + hatj + 3hatk` and which passes through the point (5, –2, 4), is `(x - 5)/2 = (y + 2)/(-1) = (z - 4)/3`.
