Advertisements
Advertisements
Question
Find the mean and the median of: 2, 4, 5, 8, 10,13 and 14
Solution
Given data = 2, 4, 5, 8, 10, 13 and 14
Clearly, middle term is 8
∴ Median = 8
∴ Mean = `"sum of observations"/"Number of observations"`
`= (2 + 4 + 5 +8 + 10 + 13 + 14)/7 = 56/7 = 8`
APPEARS IN
RELATED QUESTIONS
Find the mode and the median of the following frequency distribution:
| x | 10 | 11 | 12 | 13 | 14 | 15 |
| f | 1 | 4 | 7 | 5 | 9 | 3 |
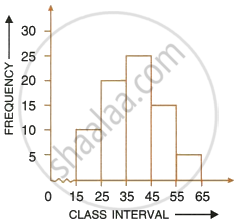
Using the information given in the adjoining histogram, calculate the mean.
The following table given the weekly of workers in a factory:
| Weekly wages (in Rs) | No.of workers |
| 50-55 | 5 |
| 55-60 | 20 |
| 60-65 | 10 |
| 65-70 | 10 |
| 70-75 | 9 |
| 75-80 | 6 |
| 80-85 | 12 |
| 85-90 | 8 |
Calcculate: (1)the mean, (2) the model class, (3) th number of workers getting weekly qages below Rs. 80 and (4) the number of workers getting Rs. 65 or more but less than Rs.85 as weekly wages.
The heights of 9 persons are 142 cm, 158 cm, 152 cm, 143 cm, 139 cm, 144 cm, 146 cm, 148 cm and 151 cm. Find the mean height.
Find the mean of the following frequency distribution :
| Class | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
| Frequency | 6 | 10 | 8 | 12 | 4 |
The mean of the following frequency distribution is 25.8 and the sum of all the frequencies is 50. Find x and y.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 7 | x | 15 | y | 10 |
The marks of 200 students in a test is given below :
| Marks% | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 |
| No. of Students | 7 | 11 | 20 | 46 | 57 | 37 | 15 | 7 |
Draw an ogive and find the number of students who scored more than 35% marks
Find the mean of: 7, 10, 4 and 17
Find the median of the following sets of numbers.
15, 8, 14, 20, 13, 12, 16
The marks in a subject for 12 students are as follows:
31, 37, 35, 38, 42, 23, 17, 18, 35, 25, 35, 29
For the given data, find the median
