Advertisements
Advertisements
Question
If θ < 90°, find the value of: `tan^2θ - (1)/cos^2θ`
Solution
Since θ <90°,
Consider θ = 45°
∴ `tan^2 θ - (1)/cos^2θ`
= `tan^2 45° - (1)/(cos^2 45°)`
= `(1)^2 - (1)/(1/sqrt(2))^2`
= `1 - (1)/(1/2)`
= 1 - 2
= -1.
APPEARS IN
RELATED QUESTIONS
Solve for x : cos2 30° + cos2 x = 1
If A = 30°, verify that cos2θ = `(1 - tan^2 θ)/(1 + tan^2 θ)` = cos4θ - sin4θ = 2cos2θ - 1 - 2sin2θ
Find the value of 'x' in each of the following: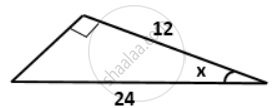
Evaluate the following: sin31° - cos59°
Evaluate the following: sec16° tan28° - cot62° cosec74°
Evaluate the following: sin22° cos44° - sin46° cos68°
Evaluate the following: sin35° sin45° sec55° sec45°
Evaluate the following: `(sin0° sin35° sin55° sin75°)/(cos22° cos64° cos58° cos90°)`
Evaluate the following: `(2sin25° sin35° sec55° sec65°)/(5tan 29° tan45° tan61°) + (3cos20° cos50° cot70° cot40°)/(5tan20° tan50° sin70° sin40°)`
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
