Advertisements
Advertisements
Question
If cot α = `1/2`, sec β = `(-5)/3`, where π < α < `(3pi)/2 and pi/2` < β < π, find the value of tan(α + β). State the quadrant in which α + β terminates.
Solution
Given that cot α = `1/2` where π < α < `(3pi)/2` (i.e,. α lies in third quadrant)
tan α = `1/(1/2)` = 2 [∵ In 3rd quadrant tan α is positive]
Also given that sec β = `(-5)/3` where `pi/2` < β < π (i.e., β lies in second quadrant cos β and tan β are negative)
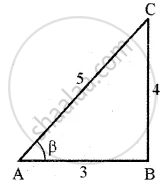
BC = `sqrt(5^2 - 3^2)` = 4
Now cos β = `1/(sec beta) = (-3)/5`
∴ tan β = `(- "Opposite side")/("Hypotenuse") = - 4/3`
Consider tan(α + β) = `(tan alpha + tan beta)/(1 - tan alpha tan beta)`
`= (2 + ((-4)/3))/(1 - 2((-4)/3))`
`= ((2xx 3 - 4)/3)/(1 + 8/3)`
`= (2/3)/(11/3)`
`= 2/11`
tan (α + β) = `2/11` which is positive.
α + β terminates in first quandrant.
APPEARS IN
RELATED QUESTIONS
Find the value of the following:
cos2 15° – sin2 15°
Prove that 2 tan 80° = tan 85° – tan 5°.
Prove that:
sin(A + 60°) + sin(A – 60°) = sin A.
If sin A = `12/13`, find sin 3A.
Prove that cot 4x (sin 5x + sin 3x) = cot x(sin 5x - sin 3x).
Find the value of sin 75°.
If cos (α + β) = `4/5` and sin (α - β) = `5/13` where (α + β) and (α - β) are acute, then find tan 2α.
The value of sin 28° cos 17° + cos 28° sin 17°
If sin A + cos A = 1 then sin 2A is equal to:
If tan A = `1/2` and tan B = `1/3` then tan(2A + B) is equal to:
