Question

If cot α = `1/2`, sec β = `(-5)/3`, where π < α < `(3pi)/2 and pi/2` < β < π, find the value of tan(α + β). State the quadrant in which α + β terminates.

Answer 1

Given that cot α = `1/2` where π < α < `(3pi)/2` (i.e,. α lies in third quadrant)

tan α = `1/(1/2)`  = 2 [∵ In 3rd quadrant tan α is positive]

Also given that sec β = `(-5)/3` where `pi/2` < β < π (i.e., β lies in second quadrant cos β and tan β are negative)

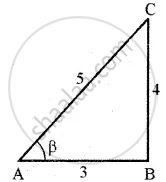
BC = `sqrt(5^2 - 3^2)` = 4

Now cos β = `1/(sec beta) = (-3)/5`

∴ tan β = `(- "Opposite side")/("Hypotenuse") = - 4/3`

Consider tan(α + β) = `(tan alpha + tan beta)/(1 - tan alpha tan beta)`

`= (2 + ((-4)/3))/(1 - 2((-4)/3))`

`= ((2xx 3 - 4)/3)/(1 + 8/3)`

`= (2/3)/(11/3)`

`= 2/11`

tan (α + β) = `2/11` which is positive.

α + β terminates in first quandrant.