Advertisements
Advertisements
Question
If cos (α + β) = `4/5` and sin (α - β) = `5/13` where (α + β) and (α - β) are acute, then find tan 2α.
Solution
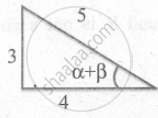
cos (α + β) = `4/5`
sin (α + β) = `3/5`
tan (α + β) = `3/4`
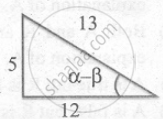
sin (α - β) = `5/13`
cos (α - β) = `12/13`
tan (α - β) = `5/12`
Now tan 2α = tan [(α + β) + (α - β)]
`= (tan (α + β) + (α - β))/(1 - tan (α + β) tan(α - β))`
`[tan (x + y) = (tan x + tan y)/(1 - tan x tan y)]`
`= (3/4 + 5/12)/(1 - (3/4)(5/12))`
`= ((9 + 5)/12)/((48 - 15)/48)`
`= (14/12)/(33/48)`
`= 14/12 xx 48/33`
`= (14 xx 4)/33`
`therefore tan (2alpha) = 56/33`
APPEARS IN
RELATED QUESTIONS
Find the value of the following:
cos2 15° – sin2 15°
If cos A = `13/14` and cos B = `1/7` where A, B are acute angles prove that A – B = `pi/3`
If cot α = `1/2`, sec β = `(-5)/3`, where π < α < `(3pi)/2 and pi/2` < β < π, find the value of tan(α + β). State the quadrant in which α + β terminates.
If A + B = 45°, prove that (1 + tan A) (1 + tan B) = 2 and hence deduce the value of tan 22`1/2`.
If sin A = `3/5`, find the values of cos 3A and tan 3A.
Find the value of tan `pi/8`.
If sin A = `1/3`, sin B = `1/4` then find the value of sin (A + B) where A and B are acute angles.
The value of sin 28° cos 17° + cos 28° sin 17°
The value of 1 – 2 sin2 45° is:
If p sec 50° = tan 50° then p is:
