Advertisements
Advertisements
Question
If an object far away from a convex mirror moves towards the mirror, the image also moves. Does it move faster, slower or at the same speed as compared to the object?
Solution
The image of the object moves slower compared to the object. It can be explained using the mirror formula :
\[\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\]
We know that for a convex mirror, the object distance (u) is positive, image distance (v) is negative and the focal length (f) is also negative. Thus mirror formula of a convex mirror is:
\[\frac{1}{u} - \frac{1}{v} = - \frac{1}{f}\]
As u = +ve
\[\frac{1}{v} - \frac{1}{f} > 0\]
\[\frac{1}{v} > \frac{1}{f}\]
\[v < f\]
Therefore, the image is always formed within the focal length of the mirror. Thus, the distance moved by the image is much slower than the distance moved by the object.
APPEARS IN
RELATED QUESTIONS
Can mirrors give rise to chromatic aberration?
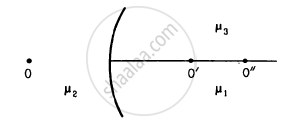
Following figure shows three transparent media of refractive indices \[\mu_1 , \mu_2 \text{ and } \mu_3\]. A point object O is placed in the medium \[\mu_2\]. If the entire medium on the right of the spherical surface has refractive index \[\mu_3\], the image forms at O". In the situation shown,
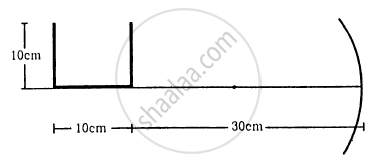
A U-shaped wire is placed before a concave mirror having radius of curvature 20 cm as shown in figure. Find the total length of the image.
A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1.33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface?
A diverging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself?
A converging lens of focal length 12 cm and a diverging mirror of focal length 7.5 cm are placed 5.0 cm apart with their principal axes coinciding. Where should an object be placed so that its image falls on itself?
A converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
A converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination .
Two thin lenses having optical powers of -10D and+ 6D are placed in contact with each other. The focal length of the combination is:
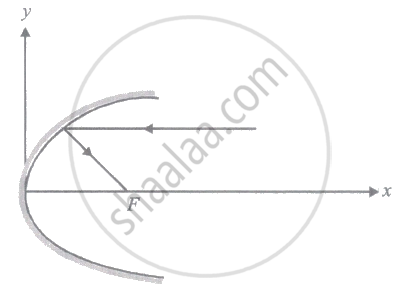
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
The radius of curvature of the curved surface of a plano-convex lens is 20 cm. If the refractive index of the material of the lens be 1.5, it will ______.
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v – f|.
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0, 0) and an object placed at (– 50 cm, 0). Find the coordinates of the image.
An object is 20 cm away from a concave mirror and it is within the focal length of the mirror. If the mirror is changed to a plane mirror, the image moves 15 cm closer to the mirror.
Focal length of the concave mirror is ______.
If an object is placed at a distance of 10 cm in front of a concave mirror of a focal length of 20 cm, the image formed will be ______.
Why does a car driver use a convex mirror as a rear-view mirror?
