Question

Suppose you are inside the water in a swimming pool near an edge. A friends is standing on the edge. Do you find your friend taller or shorter than his usual height?

Answer 1

When viewed from the water, the friend will seem taller than his usual height.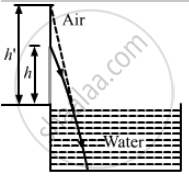

Let actual height be h and the apparent height be h'.
Here, the refraction is taking place from rarer to denser medium and a virtual image is formed.
Using
\[\frac{\mu_1}{- u} + \frac{\mu_2}{v} = \frac{\mu_2 - \mu_1}{R}\]
Where refractive index of water is μ₂ and refractive index of air is μ₁.
u and v are object and image distances, respectively.
R  is the radius of curvature, here we will take it as ∞.

\[\frac{\mu_1}{- u} + \frac{\mu_2}{v} = \frac{\mu_2 - \mu_1}{\infty}\] 

\[\frac{\mu_1}{u} = \frac{\mu_2}{v}\] 

\[v = \frac{\mu_2}{\mu_1} \times u\]
We know magnification is given by:
\[m = \frac{v}{u}\]
Putting the value of v in the above equation:

\[m = \frac{u \times \mu_2}{u}\] 

\[m =  \mu_2 \] 
As the magnification is greater than 1, so the apparent height seems to be greater than actual height.