Advertisements
Advertisements
Question
If the radii of two circles are in the ratio of 4 : 3, then their areas are in the ratio of ______.
Options
4 : 3
8 : 3
16 : 9
9 : 16
Solution
If the radii of two circles are in the ratio of 4 : 3, then their areas are in the ratio of 16 : 9.
Explanation:
Let radii of circles are r1 and r2
Given: `r_1/r_2 = 4/3`
`(pir_1^2)/(pir_2^2) = r_1^2/r_2^2`
= `(r_1/r_2)^2`
= `(4/3)^2`
= `16/9`
APPEARS IN
RELATED QUESTIONS
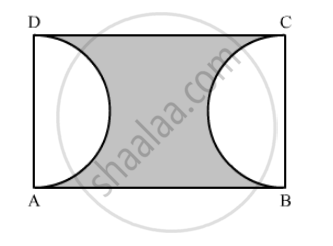
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
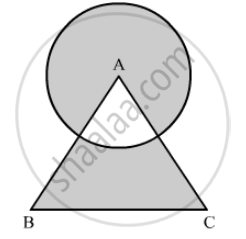
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
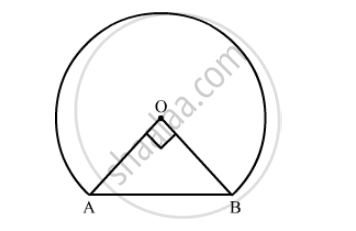
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
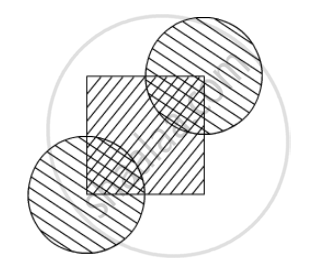
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
If the difference between the circumference and radius of a circle is 37 cm, then its area is
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

The radius of a wheel is 0.25 m. How many revolutions will it make in covering 11 km?
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
