Advertisements
Advertisements
Questions
In an AP, given a = 2, d = 8, and Sn = 90, find n and an.
Let there be an A.P. with the first term 'a' and the common difference 'd'. If an a denotes the nth term and Sn is the sum of the first n terms, find.
n and an, if a = 2, d = 8, and Sn = 90.
Solution 1
Given that a = 2, d = 8, and Sn = 90
`"As" S_n = n/2 [2a + (n - 1)d]`
`90 = n/2 [2xx2 + (n - 1)8]`
90 × 2 = 4n + n(11 - 1) × 8
180 = 4n + 8n2 - 8n
180 = 8n2 - 4n
45 = 2n2 - n
2n2 - n - 45 = 0
2n2 - 10n + 9n - 45 = 0
2n (n - 5) + 9(n - 5) = 0
(2n + 9) (n - 5) = 0
∴ Either 2n + 9 = 0
n = `-9/2`
or n - 5 = 0
n = 5
But n = `9/2` is not possible.
∴ n = 5
Now, an = a + (n - 1)d
a5 = 2 + (5 -1) × 8
a5 = 2 + 32
a5 = 34
Thus, n = 3 and a5 = 34
Solution 2
Here, we have an A.P. whose first term (a), the common difference (d) and the sum of the first n terms are given. We need to find the number of terms (n) and the nth term (an).
Here,
First term (a) = 2
The sum of the first nth terms (`S_n`) = 90
Common difference (d) = 8
So, to find the number of terms (n) of this A.P., we use the following formula for the sum of n terms of an A.P
`S_n = n/2 [2a + (n - 1)d]`
Where a is the first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
So, using the formula for n = 8, we get,
`S_n = n/2 [2(2) + (n-1)(8)]]`
`90 = n/2 [4 + 8n - 8]`
90(2) = n[8n - 4]
`180 = 8n^2 - 4n`
Further solving the above quadratic equation,
`8n^2 - 4n - 180 = 0`
`2n^2 - n - 45 = 0`
Further solving for n,
`2n^2 - 10n + 9n - 45 = 0`
2n(n - 5) + 9(n - 5) = 0
(2n + 9)(n - 5) = 0
Now
2n + 9 = 0
2n = -9/2
Also
n - 5 = 0
n = 5
Since n cannot be a fraction,
Thus, n = 5
Also, we will find the value of the nth term (an) using the formula `a_n = a + (n - 1)d`
So, substituting the values in the above-mentioned formula
`a_n = 2 + (5 - 1)8`
`a_n = 2 + (4)(8)`
`a_n = 2 + 32`
`a_n = 34`
Therefore, for the given A.P n = 5 and `a_n = 34`
APPEARS IN
RELATED QUESTIONS
The sum of n, 2n, 3n terms of an A.P. are S1 , S2 , S3 respectively. Prove that S3 = 3(S2 – S1 )
Show that a1, a2,..., an... form an AP where an is defined as below:
an = 3 + 4n
Also, find the sum of the first 15 terms.
Show that a1, a2,..., an... form an AP where an is defined as below:
an = 9 − 5n
Also, find the sum of the first 15 terms.
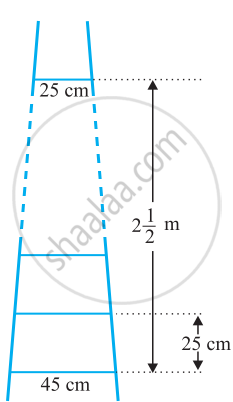
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Find the sum of the first 11 terms of the A.P : 2, 6, 10, 14, ...
If the 10th term of an AP is 52 and 17th term is 20 more than its 13th term, find the AP
Find the 6th term form the end of the AP 17, 14, 11, ……, (-40).
The 4th term of an AP is zero. Prove that its 25th term is triple its 11th term.
The 4th term of an AP is 11. The sum of the 5th and 7th terms of this AP is 34. Find its common difference
Choose the correct alternative answer for the following question .
The sequence –10, –6, –2, 2,...
Choose the correct alternative answer for the following question .
First four terms of an A.P. are ....., whose first term is –2 and common difference is –2.
Find the sum (−5) + (−8)+ (−11) + ... + (−230) .
x is nth term of the given A.P. an = x find x .
Q.11
Q.16
Q.18
Q.19
If a = 6 and d = 10, then find S10
Yasmeen saves Rs 32 during the first month, Rs 36 in the second month and Rs 40 in the third month. If she continues to save in this manner, in how many months will she save Rs 2000?
Find the sum of all even numbers from 1 to 250.
