Advertisements
Advertisements
Question
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
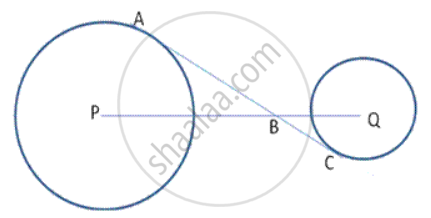
Solution
To find :- PQ
Let BC= x cm
∴ AC= 8 + x
By Pythagcras theorem BQ = `sqrt ("x"^2 + 9)`
AC2 = PQ2 -92
`=> (8 + "x")^2 = (10 + sqrt ("x"^2 + 9))^2 - 81`
`=> 64 + "x"^2 + 16"x" = 100 + "x"^2 + 9 + 20 sqrt ("x"^2 + 9)`
`=> 5 sqrt ("x"^2 + 9) = 9 + 4"x"`
Squaring both sides
⇒ 25(x2 + 9) = 81 + l6x2 + 72x
⇒ 9x2 - 72x - 144 = 0
⇒ x2 - 8x - 16 = 0
(x - 4)2 = 0
⇒ x = 4
BQ = `sqrt (4^2 + 9) = sqrt 25 = 5`
⇒ PQ = PB + BQ
⇒ PQ = 10 + 5
⇒ PQ = 15 cm
APPEARS IN
RELATED QUESTIONS
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
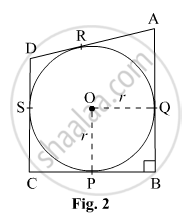
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
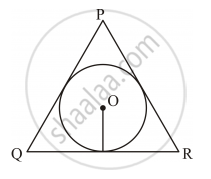
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
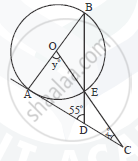
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
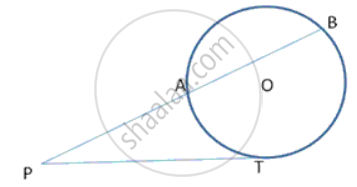
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

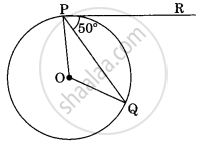
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.