Advertisements
Advertisements
Question
In the following triangle, find the value of x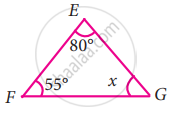
Solution
Let ∠G = x
By angle sum property we know that,
∠E + ∠F + ∠G = 180°
80° + 55° + x = 180°
135° + x = 180°
x = 45°
APPEARS IN
RELATED QUESTIONS
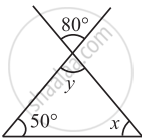
Find the value of the unknown x and y in the following diagram:
In the following triangle, find the value of x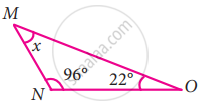
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is ______.
Can a triangle have two obtuse angles? Give reason for your answer.
Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
In a right-angled triangle, the angles other than the right angle are ______.
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
It is possible to have a triangle in which each angle is greater than 60°.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
