Advertisements
Advertisements
Question
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}.
Find: \[D - A\]
Solution
Given:
A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}
\[D - A\]= {5, 10, 20}
APPEARS IN
RELATED QUESTIONS
Draw appropriate Venn diagram for the following:
A' ∩ B'
Draw a Venn diagram for the truth of the following statement :
All rational number are real numbers.
If A and B are two sets such that \[A \subset B\] then find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cap B \right) \cap \left( B \cap C \right)\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cup D \right) \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[A \cap C\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap D\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - C\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find:
\[B - A\]
Take the set of natural numbers from 1 to 20 as universal set and show set Y using Venn diagram.
Y = {y | y ∈ N, y is prime number from 1 to 20}
Express the truth of each of the following statements using Venn diagrams:
(a) No circles are polygons
(b) Some quadratic equations have equal roots
Using the Venn diagram, examine the logical equivalence of the following statements:
(a) Some politicians are actors.
(b) There are politicians who are actors.
(c) There are politicians who are not actors.
From the given diagram find :
A ∪ B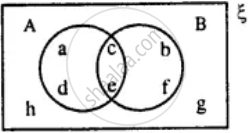
From the given diagram find :
A - B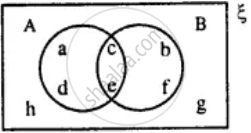
From the given diagram find :
B - A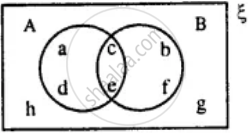
Use the given diagram to find:
(i) A ∪ (B ∩ C)
(ii) B - (A - C)
(iii) A - B
(iv) A ∩ B'
Is A ∩ B' = A - B?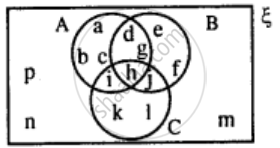
Use the given Venn-diagram to find :
B'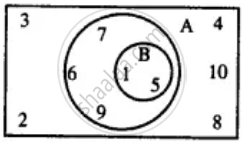
Use the given Venn-diagram to find :
A ∩ B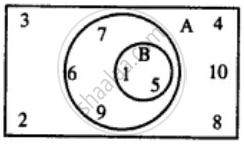
Use the given Venn-diagram to find :
A ∪ B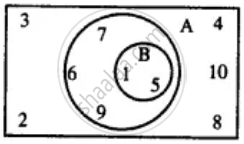
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∪ B
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
(A ∪ B)'
State the sets representing by the shaded portion of following venn-diagram :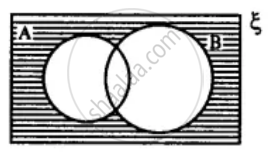
Using the given diagram, express the following sets in the terms of A and B. {g, h}
Represent the truth of the following statement by the Venn diagram.
Some hardworking students are obedient.
Represent the truth of the following statement by the Venn diagram.
No circles are polygons.
Represent the truth of the following statement by the Venn diagram.
All teachers are scholars and scholars are teachers.
Represent the following statement by the Venn diagram.
Some non-resident Indians are not rich.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
There is no student who studies both Mathematics and English.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
Some of the students study Mathematics but do not study English, some study English but do not study Mathematics, and some study both.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
Not all students study Mathematics, but every students studying English studies Mathematics.
Draw Venn diagram for the following:
Some doctors are rich
Draw Venn diagram for the following:
Some students are not scholars
