Advertisements
Advertisements
Question
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[A \cap C\]
Solution
\[A = \left\{ x: x \in N \right\} = {1, 2, 3, . . . }\]
\[B = \left\{ x: x - 2n, n \in N \right\} = {2, 4, 6, 8, . . . } \]
\[C = \left\{ x: x = 2n - 1, n \in N \right\} = {1, 3, 5, 7, . . . }\]
\[\] D = {x:x is a prime natural number.} = {2, 3, 5, 7,...}
\[A \cap C\]
APPEARS IN
RELATED QUESTIONS
Express the truth of each of the following statements by Venn diagram:
(a) Some hardworking students are obedient.
(b) No circles are polygons.
(c) All teachers are scholars and scholars are teachers.
Draw appropriate Venn diagram for the following:
A' ∩ B'
Draw appropriate Venn diagram for the following:
(A ∩ B)'
If A and B are two set such that \[A \subset B\]then find:
\[A \cap B\]
If A and B are two sets such that \[A \subset B\] then find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cap B \right) \cap \left( B \cap C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\]and D = {x : x is a prime natural number}. Find: \[A \cap B\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - C\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}.
Find: \[D - A\]
Represent the union of two sets by Venn diagram for the following.
A = {3, 4, 5, 7} B = {1, 4, 8}
Express the truth of the following statements with the help of Venn diagram:
(a) No circles are polygon
(b) If a quadrilateral is rhombus , then it is a parallelogram .
Express the truth of each of the following statements by Venn diagram :
(a) Some hardworking students are obedient.
(b) No circles are polygons.
(c) All teachers are scholars and scholars are teachers.
From the given diagram find :
A ∪ B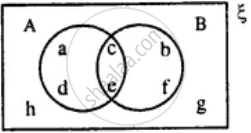
From the given diagram find :
(A ∪ B)'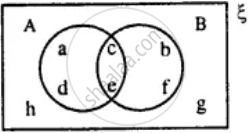
From the given diagram, find:
(i) A’
(ii) B’
(iii) A' ∪ B'
(iv) (A ∩ B)'
Is A' ∪ B' = (A ∩ B)' ?
Also, verify if A' ∪ B' = (A ∩ B)'.
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∩ B
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
B - A
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
B' ∩ A
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
(A ∪ B)'
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
B - A
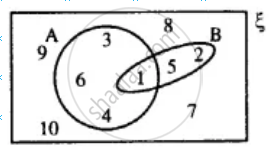
State the sets representing by the shaded portion of following venn-diagram :
In the given diagram, shade the region which represents the set given underneath the diagrams: (B - A)'
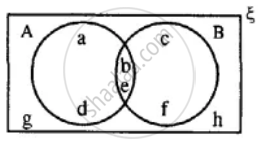
Using the given diagram, express the following sets in the terms of A and B. {a, d, c, f, g, h}
Represent the truth of the following statement by the Venn diagram.
All teachers are scholars and scholars are teachers.
Draw a Venn diagram for the truth of the following statement.
Some share brokers are chartered accountants.
Represent the following statement by the Venn diagram.
No circle is rectangle.
Represent the following statement by the Venn diagram.
If n is a prime number and n ≠ 2, then it is odd.
Express the truth of the following statement by the Venn diagram.
All men are mortal.
Express the truth of the following statement by the Venn diagram.
Some persons are not politician.
Draw Venn diagram for the following:
Some doctors are rich
