Advertisements
Advertisements
Question
Obtain the equation for lateral displacement of light passing through a glass slab.
Solution
- When a ray of light passes through a glass slab it refracts at two refracting surfaces.
- When the light ray enters the slab it travels from a rarer medium (air) to a denser medium (glass), results in deviation of ray towards the normal. When the light ray leaves the slab it travels from denser medium to rarer medium resulting in deviation of ray away from the normal.

Refraction in glass slab - After the two refractions, the emerging ray has the same direction as that of the incident ray on the slab with a lateral displacement or shift L.
- Consider a glass slab of thickness and refractive index n is kept in air medium.
- In the right angle triangle ∆ BCE,
sin (i – r) = `"L"/"BC"`;
BC = `"L"/(sin ("i - r"))` ....(1) - In the right angle triangle ∆ BCF, ....(2)
cos(r) = `"t"/"BC"`;
BC = `"t"/(cos ("r"))`
Equating equations (1) & (2)
`"L"/(sin ("i - r")) = "t"/(cos ("r"))` - After rearranging,
L = `"t" [(sin ("i - r"))/(cos ("r"))]`
APPEARS IN
RELATED QUESTIONS
Light of wavelength 5000 Å propagating in air gets partly reflected from the surface of water. How will the wavelengths and frequencies of the reflected and refracted light be affected?
A diver under water, looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than what he actually is?
Light incident normally on a plane mirror attached to a galvanometer coil retraces backward as shown in Figure. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?

A glass lens of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid?
A pole of length 1.00 m stands half dipped in a swimming pool with water level 50.0 cm higher than the bed. The refractive index of water is 1.33 and sunlight is coming at an angle of 45° with the vertical. Find the length of the shadow of the pole on the bed.
Locate the image formed by refraction in the situation shown in figure.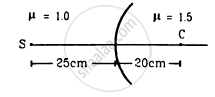
A point ‘O’ marked on the surface of a glass sphere of diameter 20 cm is viewed through glass from the position directly opposite to the point O. If the refractive index of the glass is 1.5, find the position of the image formed. Also, draw the ray diagram for the formation of the image.
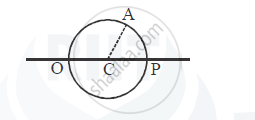
A light travels through water in the beaker. The height of water column is 'h'. Refractive index of water is 'μw'. If c is velocity of light in air, the time taken by light to travel through water will ______.
A concave mirror of focal length 'f1' is placed at a distance 'd' from a convex lens of focal length 'f2'. A parallel beam of light coming from infinity parallel to principal axis falls on the convex lens and then after refraction falls on the concave mirror. If it is to retrace the path, the distance 'd' should be ______.
Using Huygen's wave theory, show that (for refraction of light):
`sin i/sin r = "constant"`
where terms have their usual meaning. You must draw a neat and labelled diagram.
