Advertisements
Advertisements
Question
Prove by vector method that sin(α + ß) = sin α cos ß + cos α sin ß
Solution
Let `bar"a" = bar"OA", bar"b" = bar"OB"` be the unit vectors making angles α and ß respectively with positive x-axis where A and B are as shown in the diagram
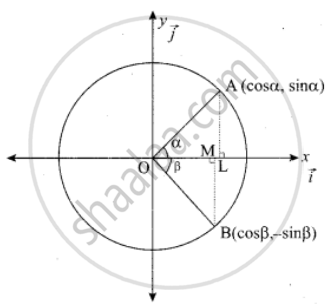
Draw AL and BM perpendicular to the X-axis, then
`"OL" = bar"OA"` = cos α
`|bar"OL"| = |bar"OA"|` cos α = cos α
`|bar"LA"| = |bar"OA"|` sin α = sin α
`|bar"OL"| = |bar"OL"| hat"j" = cos alpha hat"i"`
`bar"LA" = sin alpha(- hat"j")`
`bar"a" = bar"OA" = bar"OL" + bar"LA"`
= `cos alpha hat"i" + sin alpha hat"j"` ........(1)
Similarly `bar"b" = cos beta hat"i" - sin beta hat"j"` .......(2)
The angle between `bar"a"` and `bar"b"` is α + ß and the vectors `bar"b", bar"a", bar"k"` from a right handed system.
`bar"b" xx bar"a" = |bar"b"||bar"a"| sin(alpha + beta)hat"k"`
= `sin(alpha + beta)hat"k"` ........(1)
`bar"b" xx bar"a" = |(hat"i", bar"j", bar"k"),(cos beta, - sin beta, 0),(cos alpha, sin alpha, 0)|`
= `(sin alpha cos beta + cos alpha sin beta)hat"k"` .......(2)
From (1) and (2)
sin(α + ß) = sin α cos ß + cos α sin ß
APPEARS IN
RELATED QUESTIONS
Prove by vector method that the median to the base of an isosceles triangle is perpendicular to the base
Prove by vector method that the parallelograms on the same base and between the same parallels are equal in area
Using vector method, prove that cos(α – β) = cos α cos β + sin α sin β
Forces of magnitudes `5sqrt(2)` and `10sqrt(2)` units acting in the directions `3hat"i" + 4hat"j" + 5hat"k"` and `10hat"i" + 6hat"j" - 8hat"k"` respectively, act on a particle which is displaced from the point with position vector `4hat"i" - 3hat"j" - 2hat"k"` to the point with position vector `6hat"i" + hat"j" - 3hat"k"`. Find the work done by the forces
Find the torque of the resultant of the three forces represented by `- 3hat"i" + 6hat"j" - 3hat"k", 4hat"i" - 10hat"j" + 12hat"k"` and `4hat"i" + 7hat"j"` acting at the point with position vector `8hat"i" - 6hat"j" - 4hat"k"` about the point with position vector `18hat"i" + 3hat"j" - 9hat"k"`
Choose the correct alternative:
If `vec"a"` and `vec"b"` are parallel vectors, then `[vec"a", vec"c", vec"b"]` is equal to
Choose the correct alternative:
If a vector `vecalpha` lies in the plane of `vecbeta` and `vecϒ`, then
Choose the correct alternative:
If `vec"a"*vec"b" = vec"b"*vec"c" = vec"c"*vec"a"` = 0, then the value of `[vec"a", vec"b", vec"c"]` is
Let `veca = αhati + 3hatj - hatk, vecb = 3hati - βhatj + 4hatk` and `vecc = hati + 2hatj - 2hatk` where α, β ∈ R, be three vectors. If the projection of a `veca` on `vecc` is `10/3` and `vecb xx vecc = -6hati + 10hatj + 7hatk`, then the value of α + β is equal to ______.
Let A, B, C be three points whose position vectors respectively are
`vec"a" = hat"i" + 4hat"j" + 3hat"k"`
`vec"b" = 2hat"i" + αhat"j" + 4hat"k", α ∈ "R"`
`vec"c" = 3hat"i" - 2hat"j" + 5hat"k"`
If α is the smallest positive integer for which `vec"a", vec"b", vec"c"` are noncollinear, then the length of the median, in ΔABC, through A is ______.
Let `veca = 2hati + hatj - 2hatk` and `vecb = hati + hatj`. If `vecc` is a vector such that `veca.vecc = |vecc|, |vecc - veca| = 2sqrt(2)`, angle between `(veca xx vecb)` and `vecc` is `π/6`, then the value of `|(veca xx vecb) xx vecc|` is ______.
Let `veca, vecb, vecc` be three mutually perpendicular vectors of the same magnitude and equally inclined at an angle θ, with the vector `veca + vecb + vecc`. Then, 36 cos22θ is equal to ______.
Let `veca, vecb` and `vecc` be three unit vectors such that `|veca - vecb|^2 + |veca - vecc|^2` = 8. Then find the value of `|veca + 2vecb|^2 + |veca + 2vecc|^2`
The vector `vecp` perpendicular to the vectors `veca = 2hati + 3hatj - hatk` and `vecb = hati - 2hatj + 3hatk` and satisfying the condition `vecp.(2hati - hatj + hatk)` = –6 is ______.
The value of `[veca + 2vecb - vecc, veca - vecb, veca - vecb - vecc]` is equal to the box product ______.
Let a, b, c ∈ R be such that a2 + b2 + c2 = 1. If `a cos θ = b cos(θ + (2π)/3) = c cos(θ + (4π)/3)`, where θ = `π/9`, then the angle between the vectors `ahati + bhatj + chatk` and `bhati + chatj + ahatk` is ______.
