Advertisements
Advertisements
Question
Prove the following by using the principle of mathematical induction for all n ∈ N:
(1+3/1)(1+ 5/4)(1+7/9)...`(1 + ((2n + 1))/n^2) = (n + 1)^2`
Solution
Let the given statement be P(n), i.e.,

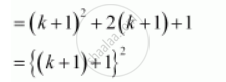
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
APPEARS IN
RELATED QUESTIONS
Prove the following by using the principle of mathematical induction for all n ∈ N:
Prove the following by using the principle of mathematical induction for all n ∈ N: x2n – y2n is divisible by x + y.
Prove the following by using the principle of mathematical induction for all n ∈ N: 41n – 14n is a multiple of 27.
Give an example of a statement P(n) which is true for all n ≥ 4 but P(1), P(2) and P(3) are not true. Justify your answer.
1 + 3 + 5 + ... + (2n − 1) = n2 i.e., the sum of first n odd natural numbers is n2.
\[\frac{1}{3 . 7} + \frac{1}{7 . 11} + \frac{1}{11 . 5} + . . . + \frac{1}{(4n - 1)(4n + 3)} = \frac{n}{3(4n + 3)}\]
1.2 + 2.3 + 3.4 + ... + n (n + 1) = \[\frac{n(n + 1)(n + 2)}{3}\]
a + (a + d) + (a + 2d) + ... (a + (n − 1) d) = \[\frac{n}{2}\left[ 2a + (n - 1)d \right]\]
32n+7 is divisible by 8 for all n ∈ N.
2.7n + 3.5n − 5 is divisible by 24 for all n ∈ N.
11n+2 + 122n+1 is divisible by 133 for all n ∈ N.
Prove that 1 + 2 + 22 + ... + 2n = 2n+1 - 1 for all n \[\in\] N .
7 + 77 + 777 + ... + 777 \[{. . . . . . . . . . .}_{n - \text{ digits } } 7 = \frac{7}{81}( {10}^{n + 1} - 9n - 10)\]
\[\text{ Given } a_1 = \frac{1}{2}\left( a_0 + \frac{A}{a_0} \right), a_2 = \frac{1}{2}\left( a_1 + \frac{A}{a_1} \right) \text{ and } a_{n + 1} = \frac{1}{2}\left( a_n + \frac{A}{a_n} \right) \text{ for } n \geq 2, \text{ where } a > 0, A > 0 . \]
\[\text{ Prove that } \frac{a_n - \sqrt{A}}{a_n + \sqrt{A}} = \left( \frac{a_1 - \sqrt{A}}{a_1 + \sqrt{A}} \right) 2^{n - 1} .\]
Prove by method of induction, for all n ∈ N:
2 + 4 + 6 + ..... + 2n = n (n+1)
Prove by method of induction, for all n ∈ N:
12 + 32 + 52 + .... + (2n − 1)2 = `"n"/3 (2"n" − 1)(2"n" + 1)`
Prove by method of induction, for all n ∈ N:
1.3 + 3.5 + 5.7 + ..... to n terms = `"n"/3(4"n"^2 + 6"n" - 1)`
Prove by method of induction, for all n ∈ N:
`1/(3.5) + 1/(5.7) + 1/(7.9) + ...` to n terms = `"n"/(3(2"n" + 3))`
Prove by method of induction, for all n ∈ N:
(24n−1) is divisible by 15
Prove by method of induction, for all n ∈ N:
Given that tn+1 = 5tn + 4, t1 = 4, prove that tn = 5n − 1
Prove by method of induction, for all n ∈ N:
`[(1, 2),(0, 1)]^"n" = [(1, 2"n"),(0, 1)]` ∀ n ∈ N
Answer the following:
Prove, by method of induction, for all n ∈ N
`1/(3.4.5) + 2/(4.5.6) + 3/(5.6.7) + ... + "n"/(("n" + 2)("n" + 3)("n" + 4)) = ("n"("n" + 1))/(6("n" + 3)("n" + 4))`
Answer the following:
Given that tn+1 = 5tn − 8, t1 = 3, prove by method of induction that tn = 5n−1 + 2
Prove statement by using the Principle of Mathematical Induction for all n ∈ N, that:
`sum_(t = 1)^(n - 1) t(t + 1) = (n(n - 1)(n + 1))/3`, for all natural numbers n ≥ 2.
Prove statement by using the Principle of Mathematical Induction for all n ∈ N, that:
22n – 1 is divisible by 3.
Prove by the Principle of Mathematical Induction that 1 × 1! + 2 × 2! + 3 × 3! + ... + n × n! = (n + 1)! – 1 for all natural numbers n.
Give an example of a statement P(n) which is true for all n ≥ 4 but P(1), P(2) and P(3) are not true. Justify your answer
Prove the statement by using the Principle of Mathematical Induction:
23n – 1 is divisible by 7, for all natural numbers n.
Prove the statement by using the Principle of Mathematical Induction:
n3 – 7n + 3 is divisible by 3, for all natural numbers n.
Prove the statement by using the Principle of Mathematical Induction:
For any natural number n, 7n – 2n is divisible by 5.
A sequence a1, a2, a3 ... is defined by letting a1 = 3 and ak = 7ak – 1 for all natural numbers k ≥ 2. Show that an = 3.7n–1 for all natural numbers.
Prove that, cosθ cos2θ cos22θ ... cos2n–1θ = `(sin 2^n theta)/(2^n sin theta)`, for all n ∈ N.
Show that `n^5/5 + n^3/3 + (7n)/15` is a natural number for all n ∈ N.
By using principle of mathematical induction for every natural number, (ab)n = ______.
