Advertisements
Advertisements
Question
Prove the following by using the principle of mathematical induction for all n ∈ N: 1.2 + 2.22 + 3.22 + … + n.2n = (n – 1) 2n+1 + 2
Solution
Let the given statement be P(n), i.e.,
P(n): 1.2 + 2.22 + 3.22 + … + n.2n = (n – 1) 2n+1 + 2
For n = 1, we have
P(1): 1.2 = 2 = (1 – 1) 21+1 + 2 = 0 + 2 = 2, which is true.
Let P(k) be true for some positive integer k, i.e.,
1.2 + 2.22 + 3.22 + … + k.2k = (k – 1) 2k + 1 + 2 … (i)
We shall now prove that P(k + 1) is true.
Consider
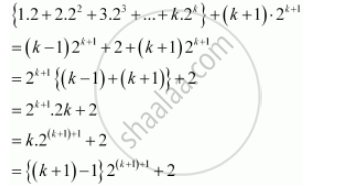
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
APPEARS IN
RELATED QUESTIONS
Prove the following by using the principle of mathematical induction for all n ∈ N:
(1+3/1)(1+ 5/4)(1+7/9)...`(1 + ((2n + 1))/n^2) = (n + 1)^2`
Prove the following by using the principle of mathematical induction for all n ∈ N:
`(1+ 1/1)(1+ 1/2)(1+ 1/3)...(1+ 1/n) = (n + 1)`
Prove the following by using the principle of mathematical induction for all n ∈ N:
`1/1.4 + 1/4.7 + 1/7.10 + ... + 1/((3n - 2)(3n + 1)) = n/((3n + 1))`
Prove the following by using the principle of mathematical induction for all n ∈ N: 41n – 14n is a multiple of 27.
If P (n) is the statement "n3 + n is divisible by 3", prove that P (3) is true but P (4) is not true.
If P (n) is the statement "2n ≥ 3n" and if P (r) is true, prove that P (r + 1) is true.
1 + 2 + 3 + ... + n = \[\frac{n(n + 1)}{2}\] i.e. the sum of the first n natural numbers is \[\frac{n(n + 1)}{2}\] .
1.2 + 2.22 + 3.23 + ... + n.2n = (n − 1) 2n+1+2
1.3 + 2.4 + 3.5 + ... + n. (n + 2) = \[\frac{1}{6}n(n + 1)(2n + 7)\]
1.2 + 2.3 + 3.4 + ... + n (n + 1) = \[\frac{n(n + 1)(n + 2)}{3}\]
52n+2 −24n −25 is divisible by 576 for all n ∈ N.
Given \[a_1 = \frac{1}{2}\left( a_0 + \frac{A}{a_0} \right), a_2 = \frac{1}{2}\left( a_1 + \frac{A}{a_1} \right) \text{ and } a_{n + 1} = \frac{1}{2}\left( a_n + \frac{A}{a_n} \right)\] for n ≥ 2, where a > 0, A > 0.
Prove that \[\frac{a_n - \sqrt{A}}{a_n + \sqrt{A}} = \left( \frac{a_1 - \sqrt{A}}{a_1 + \sqrt{A}} \right) 2^{n - 1}\]
Let P(n) be the statement : 2n ≥ 3n. If P(r) is true, show that P(r + 1) is true. Do you conclude that P(n) is true for all n ∈ N?
x2n−1 + y2n−1 is divisible by x + y for all n ∈ N.
\[\text { A sequence } x_1 , x_2 , x_3 , . . . \text{ is defined by letting } x_1 = 2 \text{ and } x_k = \frac{x_{k - 1}}{k} \text{ for all natural numbers } k, k \geq 2 . \text{ Show that } x_n = \frac{2}{n!} \text{ for all } n \in N .\]
\[\text{ A sequence } x_0 , x_1 , x_2 , x_3 , . . . \text{ is defined by letting } x_0 = 5 and x_k = 4 + x_{k - 1}\text{ for all natural number k . } \]
\[\text{ Show that } x_n = 5 + 4n \text{ for all n } \in N \text{ using mathematical induction .} \]
Prove by method of induction, for all n ∈ N:
12 + 22 + 32 + .... + n2 = `("n"("n" + 1)(2"n" + 1))/6`
Prove by method of induction, for all n ∈ N:
`1/(3.5) + 1/(5.7) + 1/(7.9) + ...` to n terms = `"n"/(3(2"n" + 3))`
Prove by method of induction, for all n ∈ N:
(23n − 1) is divisible by 7
Prove by method of induction, for all n ∈ N:
`[(1, 2),(0, 1)]^"n" = [(1, 2"n"),(0, 1)]` ∀ n ∈ N
Answer the following:
Prove, by method of induction, for all n ∈ N
8 + 17 + 26 + … + (9n – 1) = `"n"/2(9"n" + 7)`
Prove statement by using the Principle of Mathematical Induction for all n ∈ N, that:
1 + 3 + 5 + ... + (2n – 1) = n2
Prove statement by using the Principle of Mathematical Induction for all n ∈ N, that:
`(1 - 1/2^2).(1 - 1/3^2)...(1 - 1/n^2) = (n + 1)/(2n)`, for all natural numbers, n ≥ 2.
Prove by induction that for all natural number n sinα + sin(α + β) + sin(α + 2β)+ ... + sin(α + (n – 1)β) = `(sin (alpha + (n - 1)/2 beta)sin((nbeta)/2))/(sin(beta/2))`
Let P(n): “2n < (1 × 2 × 3 × ... × n)”. Then the smallest positive integer for which P(n) is true is ______.
State whether the following proof (by mathematical induction) is true or false for the statement.
P(n): 12 + 22 + ... + n2 = `(n(n + 1) (2n + 1))/6`
Proof By the Principle of Mathematical induction, P(n) is true for n = 1,
12 = 1 = `(1(1 + 1)(2*1 + 1))/6`. Again for some k ≥ 1, k2 = `(k(k + 1)(2k + 1))/6`. Now we prove that
(k + 1)2 = `((k + 1)((k + 1) + 1)(2(k + 1) + 1))/6`
Prove the statement by using the Principle of Mathematical Induction:
n3 – 7n + 3 is divisible by 3, for all natural numbers n.
Prove the statement by using the Principle of Mathematical Induction:
2n < (n + 2)! for all natural number n.
A sequence a1, a2, a3 ... is defined by letting a1 = 3 and ak = 7ak – 1 for all natural numbers k ≥ 2. Show that an = 3.7n–1 for all natural numbers.
A sequence d1, d2, d3 ... is defined by letting d1 = 2 and dk = `(d_(k - 1))/"k"` for all natural numbers, k ≥ 2. Show that dn = `2/(n!)` for all n ∈ N.
Prove that, sinθ + sin2θ + sin3θ + ... + sinnθ = `((sin ntheta)/2 sin ((n + 1))/2 theta)/(sin theta/2)`, for all n ∈ N.
Prove that number of subsets of a set containing n distinct elements is 2n, for all n ∈ N.
If 10n + 3.4n+2 + k is divisible by 9 for all n ∈ N, then the least positive integral value of k is ______.
Consider the statement: “P(n) : n2 – n + 41 is prime." Then which one of the following is true?
By using principle of mathematical induction for every natural number, (ab)n = ______.
